I recently learned about the Deuces Wild (DW) blackjack side bet from a thread started by a quizzical poster on the Wizard of Vegas message board. This side bet is trivial to describe. The outcome for DW is completely determined by the initial two cards the player is dealt. DW wins if one of the player's first two cards is a deuce, otherwise it loses. If the player's winning hand is 2/X, then the winning payout is based on the rank of the card X. This post presents DW dealt from a six-deck shoe.
The astute reader will recognize the extraordinary vulnerability of wagers based on specific cards appearing in a hand. Two similar wagers come to mind: Super Sevens (blackjack) and Lucky Nines (baccarat). However, Super Sevens is typically limited to a maximum wager of $1 and Lucky Nines is only available in an electronic version dealt from a continuous shoe. DW has no such protections.
The poster was not sure about the exact pay table for the wager, so I went searching for it online. I found a description of the game at the AGS website and a rack card. Surprisingly, neither of these provided complete information about the pay table. The available information only stated that 2/10 pays 10-to-1, 2/7 pays 7-to-1 and 2/4 pays 4-to-1.
I then located an online demonstration version of DW at the AGS website that has a full pay table imprinted on the layout. Here is the listed pay table:
- 2/A pays 11-to-1
- 2/10 pays 10-to-1
- 2/9 pays 9-to-1
- 2/8 pays 8-to-1
- 2/7 pays 7-to-1
- 2/6 pays 6-to-1
- 2/5 pays 5-to-1
- 2/4 pays 4-to-1
- 2/3 pays 3-to-1
- 2/2 pays 2-to-1
- 2/J,Q,K pays 1-to-1
- Others lose
The following table gives combinatorial analysis for DW with the pay table above:
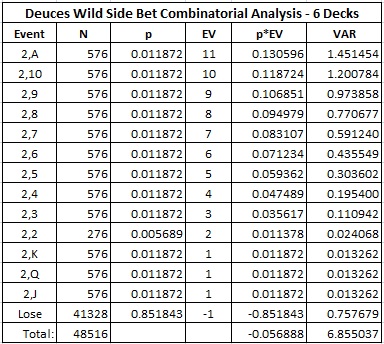
In particular:
- The house edge is 5.689%.
- The standard deviation is 2.618.
- The hit frequency is 14.816%.
The following table gives the effect of removal (EOR) for each card and a reasonable card counting system based on the EORs:
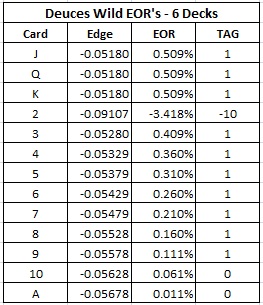
In summary, the counting system is:
- 3, 4, 5, 6, 7, 8, 9, J, Q, K = +1
- 10, A = 0
- 2 = -10
Note that in a six-deck shoe, removing a single deuce increases the house edge by over 3.4%. That's how sensitive this wager is to deuces. The betting correlation for this system is an impressive 0.992.
The following table gives the results of a simulation of one hundred million (100,000,000) six-deck shoes using the count system given above:
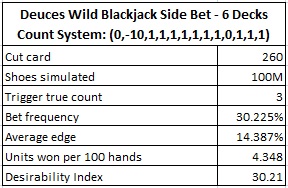
A win-rate of 4.35 units per 100 hands puts this wager in the stratosphere of card counting opportunities. I've only analyzed two blackjack side bets with a higher return. Those are Super Sevens (as mentioned above) with a win-rate of 8.55 units per 100 hands, and the "21" bet from Slingo. In some ways it is better than these competitors. With a desirability index of 30.2, DW has the highest DI of any blackjack side bet I have analyzed (see this post).
I have a brief comment about the card counting system given above. It can be simplified quite a bit without losing much power. The following card counting system has betting correlation 0.981.
- 3, 4, J, Q, K = +1
- 5, 6, 7, 8, 9, 10, A = 0
- 2 = -5
Based on a simulation of one hundred million (100,000,000) six-deck shoes, this much easier card counting system has a win-rate of 4.254 units per 100 hands. This return is over 97% of the return from the first system.
After doing this work, I learned from the original poster on the Wizard of Vegas thread that the pay table being used in the casino where he saw the game was different than that given above.
Here is the pay table found by the poster:
- 2/2 pays 20-to-1
- 2/10 pays 10-to-1
- 2/9 pays 9-to-1
- 2/8 pays 8-to-1
- 2/7 pays 7-to-1
- 2/6 pays 6-to-1
- 2/5 pays 5-to-1
- 2/4 pays 4-to-1
- 2/3 pays 3-to-1
- 2/J,Q,K,A pays 1-to-1
- Others lose
The following table gives combinatorial analysis for DW with the pay table above:
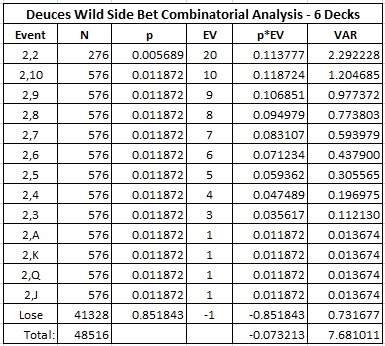
In particular:
- The house edge is 7.321%.
- The standard deviation is 2.771.
- The hit frequency is 14.816%.
The following table gives the EOR for each card and a reasonable card counting system based on the EORs:
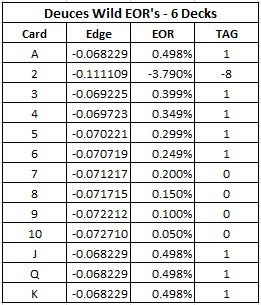
In summary, the counting system is:
- 3, 4, 5, 6, J, Q, K, A = +1
- 7, 8, 9, 10 = 0
- 2 = -8
This counting system has a betting correlation of 0.994, which is even stronger than the system for the previous pay table. The reason for this improvement is the premium payout for the hand 2/2 (20-to-1) in this pay table, whereas 2/2 only paid 2-to-1 in the previous pay table. In other words, deuces are strong as both a first card and second card. This is further reinforced by comparing the EOR for a deuce in both pay tables, 3.418% vs. 3.790%.
The following table gives the results of a simulation of one hundred million (100,000,000) six-deck shoes using the count system given above:
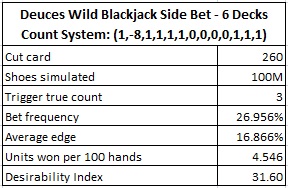
The win rate for this pay table is 4.55 units per 100 hands, which is stronger than the previous version. Even though the house edge is higher, the consistent value for the deuce makes this pay table more vulnerable to counting.
The poster stated that the maximum wager for this side bet at the casino where he found it was $25. If the AP makes a $25 DW wager whenever the true count is +3 or higher, and otherwise doesn't wager on DW, then his win rate would be about $114 per 100 hands. Assuming the AP flat bets $25 on blackjack, playing basic strategy, the AP will still earn over $100 per 100 hands.
In its present form, simply moving the cut card back will not be a sufficient remedy. Like the highly vulnerable Lucky Ladies side bet with a house edge of 24.94%, the way to save this idea is to make it as stingy as the market can bear. Of course, staff and management at the casino should also be made aware of this vulnerability so they can watch out for DW card counters. Every card counting vulnerability is safe if staff and management understand proper card counting game protection.


