During a recent trip to Las Vegas, I saw a new (to me) blackjack side bet in a downtown casino called Golden 21 (G21). What struck me as immediately suspect were events listed in the pay table corresponding to the player getting an unsuited blackjack, a suited blackjack or a suited A/K. Wagers based around blackjacks are usually very vulnerable to card counting. However, in the case of G21, there are also events in the pay table paying if the hand is a straight (consecutive ranks) or a pair, so the most obvious vulnerability was certainly mitigated.
G21 is completely resolved by the player’s first two cards. It is available in 1, 2, 6 and 8 deck versions, with numerous pay tables for each. Out of all the possible choices, I decided to investigate the particular version of G21 that seemed most vulnerable: when it is offered as a side bet in a two-deck game, using the most liberal pay table, with a 5.004% house edge.
Here are the payouts, in the order listed in pay table #5 in the available documentation:
- Unsuited blackjack pays 2-to-1.
- Suited blackjack pays 2-to-1.
- Straight (consecutive ranks, including A/2) pays 1-to-1.
- Pair pays 3-to-1.
- Straight flush (including A/2 suited) pays 6-to-1.
- Suited A/K pays 25-to-1.
- All others lose.
I have two comments:
First, all of the pay tables in the two-deck version have the same pays for unsuited and suited blackjacks, so it is redundant to list these separately on the rack card.
Second, the rack sheet states that “Only Highest Hand is Paid.” For example, A/K (offsuit) pays 2-to-1 as a blackjack and 1-to-1 as a straight. This hand is awarded only the 2-to-1 payout. I had a few minutes of challenge getting my numbers to agree with the GLI analysis (see this document) because of how the payouts are listed.
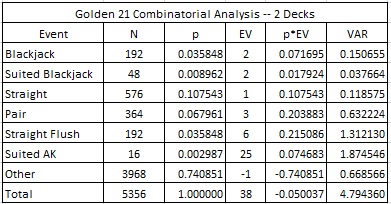
The following table gives the combinatorial analysis for G21 in the two-deck case, using pay table #5:
In particular:
- The house edge is 5.0037%.
- The hit frequency is 25.9149%.
- The standard deviation is 2.1896.
While reviewing the GLI documentation for G21, I read the following statement (click on image to make it larger):

It is refreshing to see this disclaimer in GLI’s documentation. At the very least, it gives me something to do for this blog.
The following table gives the effect of removal (EOR) for each card, together with a card counting system that closely matches the EORs:
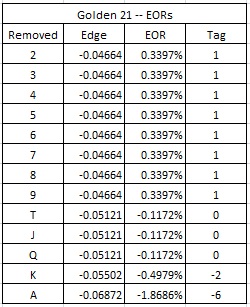
The fit of a card counting system to the EORs is measured by a metric called the “betting correlation.” For those math geeks among us, the betting correlation is the cosine of the angle between the 13-dimensional EOR vector and Tag vector. In other words, a value of 1.000 corresponds to an angle of 0 degrees, and indicates perfect correlation. The tags above have betting correlation 0.993, making this system about as good as you can get in practical terms.’
The following table shows the results for card counting G21, based on a simulation of one billion (1,000,000,000) two-deck shoes, with the cut card placed at 75 cards:
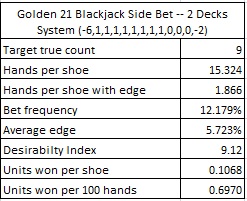
I note that the desirability index of 9.12 is based on using the standard deviation from the combinatorial analysis, which is not the same as the standard deviation that a card counter would have against this side bet. See this post for more on the desirability index for blackjack side bets.
The final result, winning 0.6970 units per 100 hands, indicates a vulnerability that is modest compared to many other blackjack side bets on the market. If a casino offers G21 with a maximum bet of $100 or less, I don’t think they should worry about it being targeted by card counters. Nevertheless, I recommend considering the possibility of card counting if a player is only playing G21 late in the shoe, and then for the table maximum.
If an AP is using “first carding”, “skilled cutting” or some other location technique, and he knows he will get an Ace or King, then clearly G21 will get his action. Every blackjack side bet is highly vulnerable to advantage play under the right constellation of circumstances. Don’t be too fixated on card counting. If you are getting pounded, then maybe something else is going on.


