A few days ago I was contacted by an advantage player who asked me to evaluate a new card counting system for Lucky Lucky (LL). I told him I would do the analysis only if he gave me permission to post the results here. He agreed. His e-mail to me was the following:
“I asked a friend last year - my nephew actually - to develop a count for Lucky Lucky, and the one he came up with was 7 = -3, A,6,8 = -2, others = +1; bet at true 2 ... how do you compare that to the counts on your site?”
I asked for more of the story from this AP about what transpired between him and his nephew. It was such an odd thing for this AP to do. Who asks their nephew? The AP replied:
"My nephew is very sharp and is good at computers, so I asked him to devise one. I asked him to compare his count to the ones on your site, but he told me he was very busy right now, and couldn't get to it soon."
I cover card counting LL in this blog post . Recall that this bet pays based on the value of the three-card hand consisting of the player’s first two cards and the dealer’s up-card. For convenience, here is a review of the most common pay tables and the house edge for each: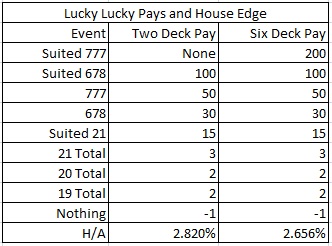
In the original post, I evaluated two systems. These were:
- “System 1” with card counting tags (-0.98, 0.90, 0.70, 0.47, 0.37, -1.21, -2.00, -1.46, 0.29, 0.73).
- “System 2” with card counting tags (-1, 1, 1, 0, 0, -1, -2, -2, 0, 1).
To this list, I added the system recommended by the nephew of the AP:
- “System 3” with card counting tags (-2, 1, 1, 1, 1, -2, -3, -2, 1, 1).
As usual for card counting systems, these tags are given in the order (A, 2, 3, 4, 5, 6, 7, 8, 9, T).
For each system, I ran a simulation of one billion (1,000,000,000) two-deck shoes and one hundred million (100,000,000) six-deck shoes. The following tables give the results of these simulations: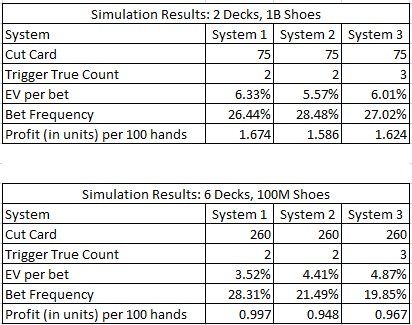
By looking at the results, it is clear that System 3 performs better than System 2 in both the two-deck and six-deck games. The player will earn 0.038 more units per 100 hands in the two-deck game and 0.019 more units per 100 hands in the six-deck game. If the player is wagering $100 on LL whenever he has the edge, then the player will earn $3.80 more per 100 hands playing the two-deck game using System 3. Likewise, the player will earn $1.90 more per 100 hands playing the six-deck game. I conclude that System 3 is an improvement over System 2.
I note that the trigger true count for System 3 is +3 and not +2, as the nephew told his AP uncle.
My opinion is that System 3 is significantly more challenging to use in practice. It is a three-level system without any neutral cards (tag = 0), whereas System 2 is a two-level system with neutral cards. But for the AP who wants to maximize his return, System 3 is certainly a strong option.
I conclude by reviewing my previous recommendations for protecting LL:
- Change the game itself. If the developers change the pay tables to give a house edge in the 5% to 10% range, this would render card counting essentially ineffective.
- Lessening the deck penetration between shuffles has minimal effectiveness, and may be cost-negative due to a reduced number of rounds per hour for legitimate play. I recommend against this remedy.
- Watch for players who place large wagers on the Lucky Lucky side bet several rounds into the shoe but don’t make a wager on the first hand.
- Watch out for team play, that is, a table full of players who are betting the Lucky Lucky bet together.
- Watch for the other usual tells that a card counting system is being used.


