At G2E (2013) last week, I came across a baccarat side bet I had not seen before at the Galaxy Gaming booth, called “Lucky Win” (LW). The side bet can be made on either the Player hand or the Banker hand and it pays when the winning hand totals 0, 1, 2, 3, or 5. A hand total in the range 0-to-5 is unlikely to win, hence the name “Lucky Win.” Imagine my surprise when I looked on the back and saw my name as a contributor to the analysis.
Here is an image showing the pertinent portion of the back side where my name is mentioned:

In particular:
“Analysis performed by respected mathematicians Mr. Charles Mousseau and Dr. Eliot Jacobson.”
With reference to the image above, the data from the Dragon Bonus downward is my analysis, but the top line discussing Lucky Win is not. To make myself perfectly clear, I did not do any work for Galaxy Gaming on the Lucky Win side bet. I did not compute any numbers at any time on any aspect of the Lucky Win side bet prior to G2E, 2013. I was not contacted about quoting my numbers or having my name on the rack sheet. I never heard of the Lucky Win baccarat side bet before G2E, 2013.
There are a number of pay tables for LW for both the Player and Banker sides. Here are the pay tables, together with the house edges, as published by Galaxy Gaming:
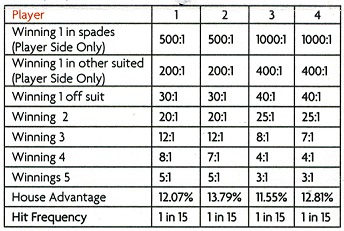
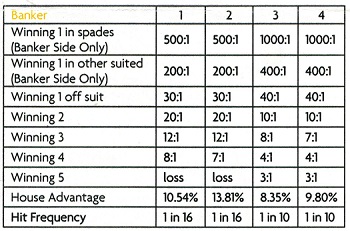
For no particular reason, I decided to focus on pay table #1 for both the Player and Banker. Here is my combinatorial analysis for pay table #1 of the Player wager:
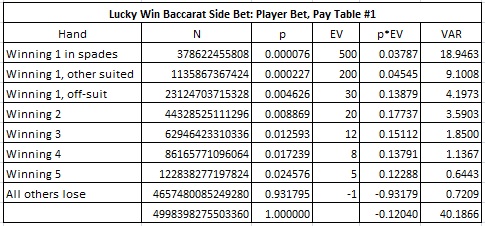
Note that I got a house edge of 12.040% for pay table #1. The rack sheet stated the house edge was 12.07%. I went on to compute the edges for the other three pay tables for the Player side and got edges of 13.764%, 11.495% and 12.750% for pay tables #2, #3 and #4, respectively. None of my numbers matched Galaxy’s. I then ran a simulation of one billion (1,000,000,000) shoes. The simulations matched my combinatorial results.
I next did the combinatorial analysis for pay table #1 of the Banker bet:
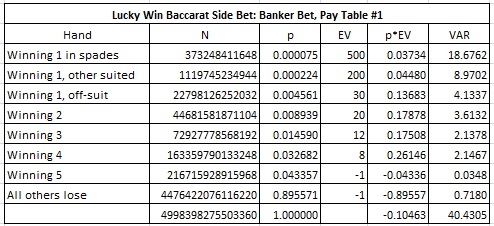
Once again, my result of 10.463% did not match the rack sheet’s value of 10.54%. For the other pay tables listed, I got edges of 13.731%, 8.193% and 9.652% respectively, again all confirmed by simulation. Okay.
Next, I turned my attention towards advantage play. To make this part easier to follow for you, I will first consider card counting the Player bet, then the Banker bet. I will finish by giving a “combined” analysis which uses a single count for both the Player and Banker bets.
To begin with, I computed the effects of removals for pay table #1 for the Player bet. I thought that spades would be important to the count, so I did a full EOR analysis by card, including suit. Here are the EOR’s:
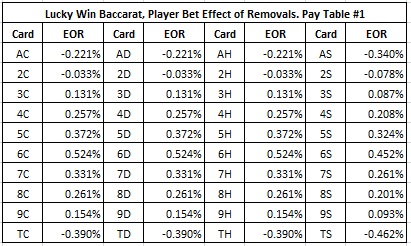
As the numbers given above show, the “Spade issue” was not such a big deal. I took the average of the EOR’s for each suit, to get an overall EOR that I used to generate the card counting tags. Here are those values and the tags:
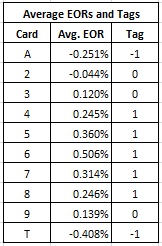
The card counting system for the Player bet is both intuitively obvious and trivially easy to use:
- 4, 5, 6, 7, 8 = +1
- 2, 3, 9 = 0
- A, T = -1
Here are the results of a simulation of one billion (1,000,000,000) shoes of baccarat, playing against pay table #1 of the Player bet, using the card counting system above, with the cut card placed at 14 cards:
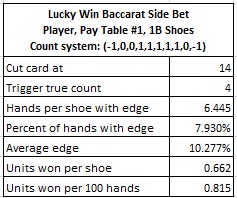
An AP who is wagering $100 whenever the true count is +4 or higher, and otherwise does not make a Lucky Win wager on the Player side, will win about $66.20 per shoe, or about $81.50 per 100 hands. This makes pay table #1 of the Player wager in LW more vulnerable to card counting than the Dragon 7 bet for EZ Baccarat (now public domain, see this post).
Next, I considered card counting against the Banker bet. Here are the EOR’s for the Banker bet, pay table #1:
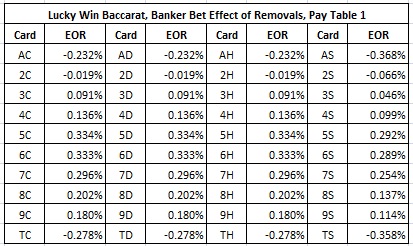
The “Spade issue” again did not materialize in any significant way. Here are the average EOR’s for each rank, taken across each row:
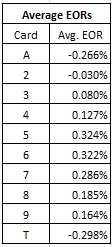
It takes just a moment’s glance to realize that the card counting system for the Player side described above works just fine for the Banker as well. While it’s true that a slightly better customized system could be created to attack the Banker wager, the simplicity and power of a single system trumps any modest increase in income.
Here are the results of a simulation of one billion (1,000,000,000) shoes of baccarat, playing against pay table #1 of the Banker bet, using the card counting system for the Player, with the cut card placed at 14 cards:
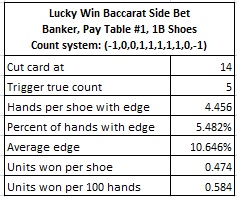
An AP who is wagering $100 whenever the true count is +5 or higher, and otherwise does not make a Lucky Win wager on the Banker side, will win about $47.40 per shoe, or about $58.40 per 100 hands.
Finally, here are the combined results. If an AP uses the counting system (-1,0,0,1,1,1,1,1,0,-1) against both the Player bet and Banker bet, using pay table #1 for each wager, then:
- The AP should make the Player bet when the true count is +4 or higher.
- The AP should make the Banker bet when the true count is +5 or higher.
- The AP will earn 0.815 units per 100 hands from his Player bets.
- The AP will earn 0.584 units per 100 hands from his Banker bets.
- Altogether, the AP will earn 1.399 units per 100 hands.
If the AP makes a $100 wager on the Player or Banker Lucky Win bets when the count indicates, and otherwise does not make a Lucky Win bet, then the AP will earn about $139.90 per 100 hands. In the spectrum of card counting opportunities against baccarat side bets, Lucky Win is one of the most vulnerable I’ve analyzed.
With this information, I now want to discuss the advantage play numbers given in Galaxy’s rack sheet. The sheet states a loss to the AP of $8.19 per 100 hands, with a $100 wager. This number understates the vulnerability by about $130 per 100 hands. The actual vulnerability is over 17-times what is stated on the rack sheet.
The rack sheet also states:
Lucky Win Baccarat is the most Count Resistant, Advantage Play, and Team Play resistant Baccarat product commercially available because of its dynamic pay table (see full analysis below)
In my opinion, this is an incorrect assessment of the vulnerability of Lucky Win to advantage play.
It is fully possible that Charles did the mathematics correctly, but his results were misunderstood by someone at Galaxy Gaming. This may very well be the case, Charles is an outstanding gaming mathematician. In a conversation with him, he indicated that he did a perfect play analysis with the cut card at 21 cards. Charles stated that he did not use my methodology for card counting analysis. The fact that a breakdown occurred is certain, The place at which it occurred is not my business.
My conclusion is that Lucky Win is highly vulnerable to card counting, nearly twice that of the Dragon 7 bet. Take strong precautions against card counting if you install Lucky Win in your casino.
Acknowledgement: Thanks to Stephen How for his confirmation of some of the results presented here,. I met Stephen at this year's G2E (2013). He is as gifted and talented as he is nice. Based on our conversations, Stephen did his own analysis which he posted today on his website, discountgambling.net.


