The Natural 9 (NAT9) side bet is the wager that the Player hand or Banker hand will be a natural 9. NAT9 is actually two different side bets, as the wager can separately be made that the Banker hand will be a natural 9 and that the Player hand will be a natural 9. Similarly, the Natural 8 (NAT8) side bet is the wager that the Player hand or Banker hand will be a natural 8. Both NAT9 and NAT8 are as old as the hills; Edward Thorp analyzed advantage play against them nearly 50 years ago (see this post) and determined that they can both be soundly defeated. In the early 1960s, in the midst of the industry-wide panic over the new army of blackjack card counters, Thorp unleashed a fresh line of attack. Nevertheless, NAT9 and NAT8 are still finding their ways into casinos worldwide.
The most common payout for both NAT9 and NAT8 is 9-to-1 for a natural. The 8-to-1 payout is seen as well. Here is the combinatorial analysis for the NAT9 side bet for both of these payouts:
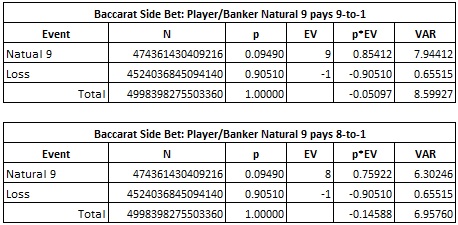
In particular,
- The house edge for NAT9 with a 9-to-1 payout is 5.097%.
- The house edge for NAT9 with an 8-to-1 payout is 14.588%.
Here is the combinatorial analysis for the NAT8 side bet for both of these payouts:
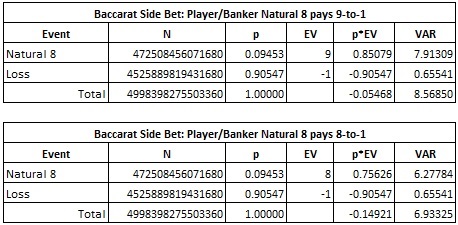
In particular,
- The house edge on NAT8 with a 9-to-1 payout is 5.468%.
- The house edge on NAT8 with an 8-to-1 payout is 14.921%.
I am going to first cover card counting against NAT9 and then move on to NAT8. I will conclude by considering a team approach to playing against both wagers simultaneously.
Natural 9
The card counting system that Thorp considered against NAT9 was simply to count nines against all other cards. In other words, the Thorp count against NAT9 is:
- 9 = -12
- All others = +1
I will denote the Thorp count by (1,1,1,1,1,1,1,1,-12,1). The following table gives the results of a simulation of one billion (1,000,000,000) shoes, using the Thorp count to count NAT9:
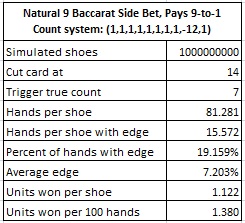
These results hold for both the Player NAT9 wager and the Banker NAT9 wager. When the true count is +7 or above, the counter should make a wager on both hands. If the card counter makes a wager of $100 on both hands whenever the true count is +7 or above and otherwise does not make a wager on NAT9, then the counter will earn $138.00 per 100 hands on each side of the wager, for a total of $276.00 per 100 hands.
There is an alternative counting system here that is worth investigating. The most common way of making a natural 9 requires both a nine and a ten-valued card (Ten, Jack, Queen, King). It is therefore reasonable to consider a count where the ten-valued cards have a neutral count. In other words:
- 9 = -8
- T, J, Q, K = 0
- A, 2, 3, 4, 5, 6, 7, 8 = +1
This count is similar to the powerful “blackjack count” used to beat the Slingo 21 blackjack side bet, where blackjack pays 19-to-1 (see this post). When I ran a simulation of one billion (1,000,000,000) shoes using this system against NAT9, the units won per 100 hands was 1.37941. With five decimal digits accuracy, the simulation of the Thorp count showed a return of 1.37991 units per 100 hands. Thorp’s system outperformed this system by a microscopic 0.00050 units per 100 hands. With a unit of $100, the Thorp system earns an extra nickel per 100 hands. The difference is statistically insignificant.
These results show that NAT9 is highly vulnerable to card counting, and that there are two very effective counting systems that can be used to crush NAT9. The usual defense to card counting is to decrease the placement of the cut card. The following table shows the card counting statistics for a variety of cut card placements using the Thorp count. Each row was obtained by a simulation of one billion (1,000,000,000) shoes.
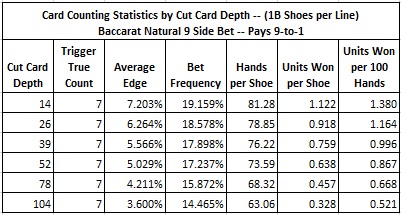
Even with a cut card at 104 cards (2 decks), the counter can earn 0.521 units per 100 hands. With a $100 unit and making wagers on both the Banker and Player bets, the counter can still beat NAT9 for $104.20 per 100 hands. This shows that cut card placement alone is not a solution to defending NAT9.
An alternative approach to strengthening the NAT9 side bet is to simply offer a reduced payout of 8-to-1. With a huge house edge of 14.588%, the counter has a mountain to climb until the edge falls his way. The following table gives the results of a simulation of one billion (1,000,000,000) shoes using the Thorp count when NAT9 pays 8-to-1:
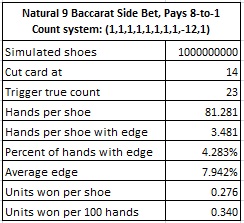
With a payout of 8-to-1, the counter can earn 0.340 units per 100 hands. With a $100 unit and making wagers on both the Banker and Player bets, the counter can beat NAT9 for $68.00 per 100 hands.
It is now clear that correct defense of the NAT9 wager involves both a reduced payout of 8-to-1 and reduced placement of the cut card. In my opinion, with a payout of 8-to-1 and the cut card placed at 52 cards (1 deck), NAT9 is effectively safe from card counting.
Natural 8
I now consider the NAT8 side bet. The card counting system that Thorp considered against NAT8 was simply to count eights against all other cards. In other words, the Thorp count against NAT8 is:
- 8 = -12
- All others = +1
I will denote the Thorp count by (1,1,1,1,1,1,1,-12,1,1). The following table gives the results of a simulation of one billion (1,000,000,000) shoes, using the Thorp count to count NAT8:
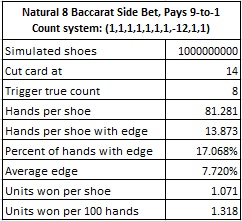
These results hold for both the Player NAT8 wager and the Banker NAT8 wager. When the true count is +8 or above, the counter should make a wager on the Player and Banker NAT8 side bet. If the card counter makes a wager of $100 on both hands whenever the true count is +8 or above and otherwise does not make a wager on NAT8, then the counter will earn $131.80 per 100 hands on both sides of the wager, for a total of $263.60 per 100 hands.
These results show that NAT8 is highly vulnerable to card counting using the Thorp count. The usual defense to card counting is to decrease the placement of the cut card. The following table shows the card counting statistics for a variety of cut card placements. Each row was obtained by a simulation of one billion (1,000,000,000) shoes.
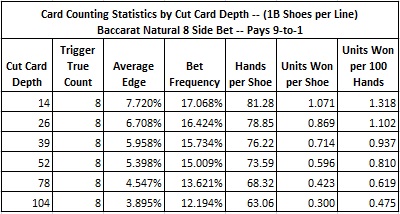
Even with a cut card at 104 cards (2 decks), the counter can still earn 0.475 units per 100 hands. With a $100 unit and making wagers on both the Banker and Player bets, the counter can beat NAT8 for $95.00 per 100 hands. This shows that cut card placement alone is not a solution to defending NAT8.
As before, by simply reducing the payout to 8-to-1, card counting is much less effective. The following table gives the results of a simulation of one billion (1,000,000,000) shoes, using the Thorp count to count NAT8 when it pays 8-to-1:
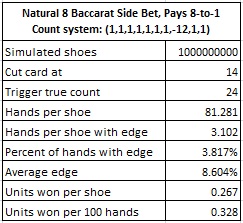
With a payout of 8-to-1, the counter can earn 0.328 units per 100 hands. With a $100 unit and making wagers on both the Banker and Player bets, the counter can beat NAT8 for $65.60 per 100 hands.
As with NAT9, the best defense for the NAT8 wager involves both a reduced payout of 8-to-1 and reduced placement of the cut card. In my opinion, with a payout of 8-to-1 and the cut card placed at 52 cards (1 deck), NAT8 is effectively safe from card counting.
Team Play
If a casino offers NAT9 and NAT8 with the 9-to-1 payout then things can go very wrong very fast. The easiest path for a solo counter to crush this combination is to use a score card and simply count the number of 8’s played, the number of 9’s played, and the total number of other cards played. With a little practice, the AP can simultaneously count both the NAT9 and NAT8 bets. Alternatively, the AP can use the help of a confederate and a team approach, where each AP keeps one of the counts. When one of the APs makes his wager, the other AP follows suit, making the same wager. In this way, both APs get the full value from making both the NAT9 and NAT8 side bets.
The following table shows the win rate for each team member against NAT9 and NAT8 when they pay 9-to-1 and the cut card is placed at 14 cards:
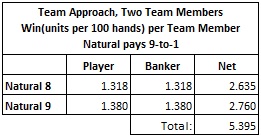
With a $100 unit, playing against both the NAT9 and NAT8 side bets, each team member will earn about $539.50 per 100 hands. The team of two APs will earn about $1079.00 per 100 hands, with a $100 unit. As mentioned above, a skilled AP could obtain this full win-rate by himself, with the help of a baccarat score card and a little practice. These win rates place the NAT9 and NAT8 side bets in elite territory among the most vulnerable ever offered at the baccarat tables.
The following table shows the win rate for team play when NAT9 and NAT8 pay 8-to-1 and the cut card is placed at 14 cards:
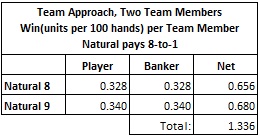
We see that each team member earns $133.60 per 100 hands. A team of two APs working together earn at a rate of$267.20 per 100 hands, with a $100 unit. For this reason, it is clear that reducing the payouts to 8-to-1 is not enough to fully protect this opportunity. Decreased cut card placement is required as well.
Edward Thorp and his colleague William Walden took advantage of a powerful opportunity in the early 1960’s to crush the NAT9 and NAT8 side bets using a simple card counting methodology. As they documented in their original paper, Thorp and Walden beat these two side bets for over $24,000. While casino staff were obsessed with the “army of blackjack card counters” who were swarming their single-deck games, Thorp and Walden were quietly burning NAT9 and NAT8 on the baccarat tables. There are still casinos all over the world where this obsessive blindness has not changed much in 50 years.
From the casino side, the NAT9 and NAT8 side bets are excellent income enhancements for baccarat. But they must be offered with great caution. My recommendations for protecting NAT9 and NAT8 are as follows:
- Only offer NAT9 and NAT8 with the 8-to-1 pay table.
- Cut off one deck when these side bets are offered.
- Watch for team play.


