A long long time ago, in a casino far far away, there was a blackjack side bet called “Over/Under 13” (OU13). The player had the opportunity to wager that his two cards would total more than 13 (Over) or would total less than 13 (Under). A total of 13 lost for both wagers. These were even-money wagers, nothing fancy.
OU13 was first offered at Caesar’s Tahoe in 1989, and became very popular by the early 1990’s. By the time I started looking at advantage play against side bets, OU13 was already long gone. I did not expect that I would ever write about it here, but that changed when I recently spotted it in an overseas casino. Although it was offered on a game that used a continuous shuffler (hence safe), the very fact that it still exists is reason enough to consider it. If it exists, a casino somewhere will find a way to screw it up.
To give an idea of how well understood advantage play is against OU13 one has to look no further than the work of the great Arnold Snyder:
Snyder goes through a great deal of analysis in his article, including computing the EORs and proposing six different card counting systems. He also writes at length about how ineffective ordinary card counting systems are when used against OU13. Snyder states:
“Although it is possible to develop many multi-parameter approaches that would optimize potential profits on both the over/under bets and the regular blackjack hand, I would not consider these more difficult strategies to be worth the trouble … The vast majority of your profit potential will come from betting accurately on your over/under opportunities. You want to play the regular blackjack hand well enough to reduce the ½% house advantage to as near a break-even point as possible.”
Snyder was pointing out that if you are playing against a side bet, then that’s what you should focus on doing. Twenty-five years later, both blackjack card counters and casino management hang on to the altar of the high-low count. Beating casino table games begins with doing whatever the math says to do.
Here are links to two articles on OU13 written by Arnold Snyder:
- A System for Beating the Over/Under Side Bet, 1989
- The Unbalanced Over/Under Card Counting System, 1991
The history of publicly available analysis OU13 does not end with Snyder. In the 1994 book, “Professional Blackjack,” written by Stanford Wong, an entire chapter is devoted to OU13:
Wong writes:
“The pioneering publication explaining how to get an edge on the over/under side bets is “The Over/Under Report,” an excellent paper by Arnold Snyder … I will introduce the counting system that I prefer to use for the over/under side bets, a system not mentioned in Snyder’s paper. It was called the crush count by Jake Smallwood in the March 1990 issue of Blackjack Monthly.”
The crush count has the following values:
- A, 2 = +2
- 3 = +1
- 4, 5, 6, 7, 8 = 0
- 9, T = -1
The same count is used for both the Over 13 and Under 13 wagers. The AP then makes an Over 13 wager whenever the true count is equal to or above some positive trigger value, and makes an Under 13 wager whenever the true count is equal to or below some negative trigger value.
In this article I am going to give the card counting performance data for the “crush count.” I am also going to do this analysis for a "much stronger" multi-level system. I do not claim any originality here, except to the extent that I am using a modern computer to get more accurate simulation numbers than were possible 20+ years ago.
The following table gives the combinatorial analysis for both the Over 13 and Under 13 wagers in a six-deck shoe game: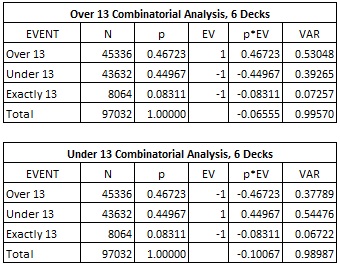
In particular:
- The house edge for the Over 13 bet is 6.555%.
- The house edge for the Under 13 bet is 10.067%.
The following tables give the values for the Effect of Removal (EOR) for both the Over 13 and the Under 13 wagers. I also give card counting tags that very closely correlate to the EOR’s (betting correlation above 0.99).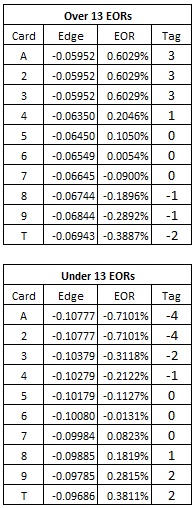
Some of these EOR’s are very large. For example, removing a single Ace from a six-deck shoe moves the house edge towards the player on the Over 13 bet by over 0.60%.
The following tables give the results of simulations of these two card counting systems in a six-deck shoe game, where the cut card is placed at 260 cards (52 cards from the end). These results were based on simulations of one hundred million (100,000,000) six-deck shoes.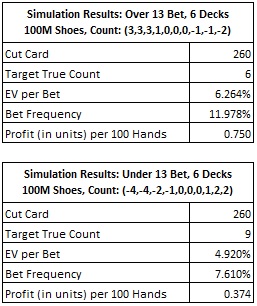
If a card counter was able to use both of these counts simultaneously, his profit per 100 hands would be 1.124 units. That’s a hefty profit by any standard, making OU13 a highly vulnerable blackjack side bet. But this is not a reasonable expectation. Another possibility is that two card counters working as a team could each keep one of these counts. For an individual AP, it is best to develop a single count that can be used for both the Over 13 and the Under 13 bet. That is exactly what the “crush count” does.
As discussed above, the crush count has tags (2,2,1,0,0,0,0,0,-1,-1). The following tables give the results of simulations of the crush counting system in a six-deck shoe game, where the cut card is placed at 260 cards (52 cards from the end). These results were based on simulations of one hundred million (100,000,000) six-deck shoes.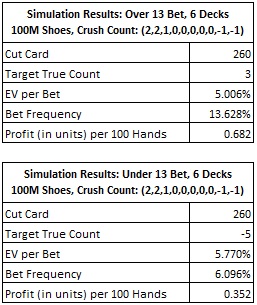
The counter makes the Over 13 bet whenever the true count is +3 or higher. He makes the Under 13 side bet whenever the true count is -5 or lower. If he does this, then:
- The EV per bet is 5.242%.
- The bet frequency is 19.724%.
- The profit in units per 100 hands is 1.034.
An AP who makes a $100 wager on either the Over 13 or Under 13 wager whenever the crush count indicates, and otherwise does not wager on OU13, will earn approximately $103.40 per 100 hands.
The very easy to use crush count yields 91.94% of the profit available by combining the two multi-level systems described earlier. I am humbled by the strength of this system and by the good work of those who analyzed and wrote about UO13 over 20 years ago.
In this modern era, there is only one reasonable way to offer OU13:
- OU13 must be offered only when using a continuous shuffle machine.


