“Time flies like an arrow. Fruit flies like a banana.”
– Unknown (not Groucho Marx)
The Over/Under 13 (OU13) blackjack side bet is actually two different side bets: the player can wager that his first two cards will total more than 13 (the “Over” bet) or less than 13 (the “Under” bet). Each wager pays even money. A total of 13 is a loss for both wagers, giving the house edge. That OU13 is countable is intuitively obvious to the casual observer. In fact, OU13 was one of the first blackjack side bets to be systematically analyzed and beaten by APs.
OU13 first appeared at Caesar’s Tahoe in 1989 and was already long gone by the time I started playing in 1996. However, like Lazarus, it has been raised from the dead. Last August I observed it being offered from a continuous shuffle machine, prompting this blog post. Then last week an advantage player (let’s call him “Fred”) wrote to me saying he saw OU13 offered on a six-deck shoe game (somewhere in the world-wide casinosphere). It’s hard to understand how a casino anywhere could offer this wager from a shoe given its long documented history of being beaten by APs. It seems the casino industry is quick to forget the hard lessons it has learned.
Here is the combinatorial analysis for OU13: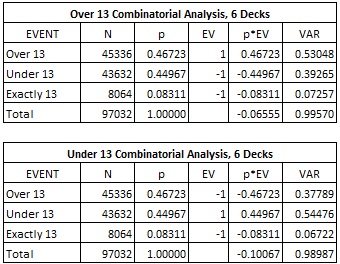
In particular, in a six-deck game, the Over 13 bet has a 6.555% house edge and the Under 13 bet has a 10.067% house edge. Because of its higher house edge, the Under 13 bet is worth less to the card counter than the Over 13 bet. Therefore, the primary focus of early advantage play analysis was on beating the Over 13 bet.
Among the early authors who wrote about card counting OU13 were Arnold Snyder and Stanford Wong (see Professional Blackjack). In particular, Wong suggested the highly effective Crush count that could be simultaneously used to count both the Over 13 and Under 13 bets:
- A, 2 = +2
- 3 = +1
- 4, 5, 6, 7, 8 = 0
- 9, T = -1
As I previously analyzed, the AP should play the Over when the true count is +3 or higher and the Under bet when the true count is -5 or lower. In this way, the Crush count yields 0.682 + 0.352 = 1.034 units per 100 hands in a six-deck game. This return places OU13 in high-risk territory for blackjack side-bets on a six-deck shoe game.
Fred asked me to analyze some “unbalanced” counts to be used against the Over 13 bet. An unbalanced count is a list of indices that adds up to some positive Integer (rather than 0). Unbalanced counts are far easier to use than balanced counts simply because there is no true count conversion. The counter starts with a running count of 0, and when the running count exceeds some trigger value, the counter makes the bet. Without the need for a true count conversion, most of the mathematical struggle can be avoided. The problem, however, is that unbalanced counts are often substantially weaker than balanced counts. But this isn’t always the case. For example, the perfect insurance count (see this post) is unbalanced.
In this article, Arnold Snyder proposed several unbalanced counts that could be used against the Over 13 wager. However, Snyder could not find dual purpose unbalanced counts, like the Crush count, that could be used for both the Over and Under wagers. Snyder wrote:
The main problem here is that I can’t come up with any easy running count method that will take advantage of both the over and under bets. Using the RWC simulation analyses, however, it’s easy to see that even with the over/under count, the significant gains in multi-deck over/under games come from the over bets. Since most of the over/under games available in casinos are shoe games, we can develop running count systems for taking advantage of the over bet only.
Here are the three systems that Snyder suggested (image captured from his article):
Note that for each count, the indices add up to +1, making them unbalanced.
I simulated one hundred million (100,000,000) six-deck shoes, using the counting systems above to play against the Over 13 bet. The following tables summarize the results of these simulations.
Here are the results for Snyder’s System #1, showing a win-rate of 0.574 units per 100 hands: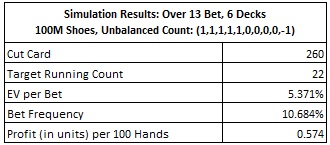
Here are the results for Snyder’s System #2, showing a win-rate of 0.621 units per 100 hands: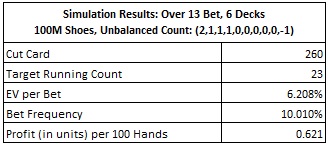
Finally, here are the results for Snyder’s System #3, showing a win-rate of 0.691 units per 100 hands: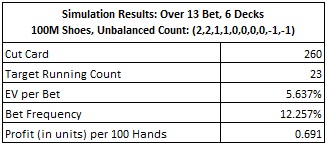
The Crush count returned 0.682 units per 100 hands on the Over 13 bet. My simulation showed that System #3 returns 0.691 units per 100 hands. In other words, System #3 outperforms the Crush count on the Over 13 wager. An AP who wants to play against the Over bet only will find System #3 both easy to use and powerful. The downside for the AP is that System #3 can’t be used to count the Under 13 wager.
One reader (JP) shared an idea he had for a count that could work for both Over 13 and Under 13 that wouldn't require a true count conversion. His idea appears to be new to the lexicon for OU13 and is something that Arnold Snyder apparently never considered when he wrote his articles.
This AP's idea is that you start with the Crush count (2,2,1,0,0,0,0,0,-1,-1) and also use a side count of 3's. That is, the AP must both keep the running count (call this value RC) for the Crush count and also keep track of how many 3's have been played from the shoe (call this value SC3). Keeping a side count is something that top APs are accustomed to doing; for example, many of the best blackjack card counting systems involve keeping a side count of Aces.
In the case of OU13, the AP uses the following: to get the "Count" for the current hand:
- If RC > 0, then Count = RC + SC3
- If RC < 0, then Count = RC - SC3
- If RC = 0, then Count = RC
That is, the AP adds the number of 3's to the running count if the running count is positive and subtracts the number of 3's from the running count if the running count is negative. The AP then uses this count to determine if he wants to make a bet. The upside to this system is that no division is required; there is no true count conversion. The downside to this system is that the AP has to keep a side count. Life is never easy, is it?
Here are the results from a simulation of 100M six-deck shoes using the counting system (Crush count with side count) above: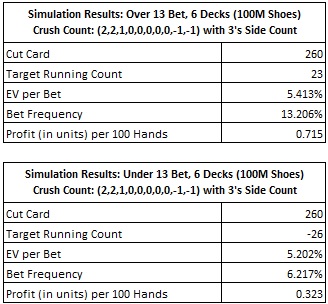
The Crush count returns 0.682 units per 100 hands on the Over 13 bet and 0.352 units per 100 hands for the Under 13 bet, for a total of 1.034 units per 100 hands. The Crush count with a side count returns 0.715 + 0.323 = 1.038 units per 100 hands, outperforming the Crush count without the need for a true count conversion.
I would like to thank JP for sharing his great idea with me. Something new!
As I concluded in my first blog post on OU13, in this modern era there is only one reasonable way to offer OU13:
- OU13 must be offered only when using a continuous shuffle machine.


