The Upcard Luck (UL) blackjack side bet is a bit wacky to describe. Payouts are based on the dealer's up-card together with the two cards the player is dealt. In this sense, it is similar to both Lucky Lucky and 21 + 3. There would certainly be intellectual property issues if this bet made it big. Right now, though, it has very few placements.
Here's how it goes. The player receives two cards and the dealer receives his two cards, with one of the cards (the dealer's up-card) face up, as usual. If the dealer's up-card is not a 2, 3, 4, 5, 6 or 7, then the player automatically loses the UL bet. Otherwise, the player's hand is considered. The player then needs either a total of 9, 10, 11, 18, 19, 20, 21 or he needs two suited Aces, to win UL. Note that Aces always count 11 in figuring out the player's two card total, so that a total of 21 is the same as blackjack.
The game developer believes this game does have a theme. Players love it when the dealer has a crappy up-card. Players love it when they get a good starting hand. This wager requires both good things to happen in order to win the bet. In other words, if either the player's starting hand sucks, or the dealer's up-card is good, the player loses his UL wager. Good compounds good and any bad is bad. The problem is, for the player there is a lot more bad than good.
The following are the payouts for the most common pay table. These payouts assume the dealer's up-card is a 2, 3, 4, 5, 6 or 7. Recall that Aces count 11.
- Player has two suited Aces, pays 60-to-1.
- Player has blackjack, pays 10-to-1.
- Player has a total of 9, 10 or 11, pays 5-to-1.
- Player has a total of 18, 19 or 20, pays 2-to-1.
- Player loses all other hands, including all hands where the dealer's up-card is an 8, 9, T, J, Q, K or A.
The following table gives the combinatorial analysis for UL with the pay table above when the game is dealt from a six-deck shoe: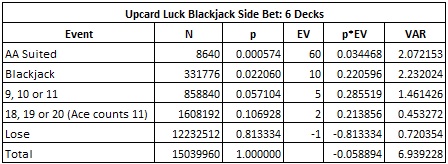
In particular,
- The house edge is 5.8894%
- The standard deviation is 2.6342
- The hit frequency is 18.6667%
There is another pay table that may be used, where a pair of suited Aces pays 50-to-1 and blackjack pays 11-to-1. I am not sure if this pay table is used. The house edge is lower and that 11-to-1 payout seems unnatural. Here is the combinatorial analysis, showing a house edge of only 4.2579%: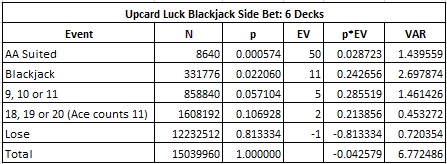
As for card counting, it should be clear that Aces are extremely important to the AP. They create the two top pays: suited AA, and blackjack. Meanwhile, the AP also wants the deck to be rich in 2, 3, 4, 5, 6, 7. After all, if the dealer doesn't turn up one of those cards, then the bet is lost. It comes as no surprise that the EORs yield a count system based around this intuition: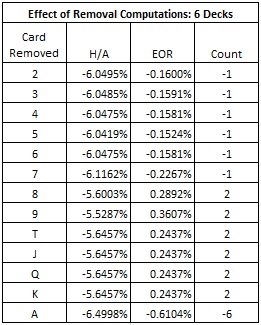
In summary:
- A = -6
- 2, 3, 4, 5, 6, 7 = -1
- 8, 9, T, J, Q, K = +2
The betting correlation for this count system is pretty solid, at 0.9759.
So, how did it do? Here are the results of a simulation of one hundred million (100,000,000) six-deck shoes using the count system above: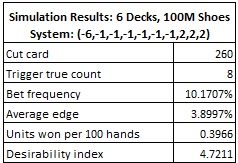
A return of 0.3966 units is pretty sad for the AP. With a DI of 4.72, only the hardiest of APs will consider playing against this bet. But, keep in mind that the return for the AP will be better if the second pay table is being used.
The documentation for this wager states that the wager on UL must not exceed the primary blackjack bet, in the author's words, "... in order to thwart card counting." In a casino that offers a $1000 maximum bet on blackjack,a player will just back count this wager, making his UL bet alongside a $1000 bet on the main game when the count is ripe. In this case, UL is quite vulnerable and the rule the game developer stated will actually encourage card counting. However, if the maximum wager on UL is $100 or less, as is likely, then don't worry about this one. Nobody's going to bother.
Well, not exactly "nobody." If an AP is tracking Aces, top-carding or shuffle tracking, then surely they could have a lot of fun with this one. The fact that James Grosjean bragged about hitting the QH,QH pair in Lucky Ladies should be evidence by itself that these guys know some good stuff.


