The Tie bet is among the safest side bets in baccarat. Various approaches have been tried in developing a strategy to defeat the tie (see this post and this post). However, even using computer perfect play and a cut card placed at 7 cards, an AP who places a $100 wager on the Tie bet whenever he has the edge will only earn about $33 per shoe (0.33 units per shoe). It is unlikely any serious AP would try to defeat the Tie bet. Such is not the case with the Tie bet variant “UR Way Egalite” (UWE). As I will show, UWE is among the most beatable games of any I have analyzed on this blog.
What distinguishes UWE is that the player can wager on each separate tie, with separate odds for each. That is, UWE is ten separate wagers, with each of the ties on 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 having a different payout. If the result of a hand is anything other than a tie, then all UWE wagers lose. The player can play none, some or all of these numbers on any given hand.
The ten separate UWE tie bets are as follows:
- Tie on 0 pays 150-to-1
- Tie on 1 pays 215-to-1
- Tie on 2 pays 225-to-1
- Tie on 3 pays 200-to-1
- Tie on 4 pays 120-to-1
- Tie on 5 pays 110-to-1
- Tie on 6 pays 45-to-1
- Tie on 7 pays 45-to-1
- Tie on 8 pays 80-to-1
- Tie on 9 pays 80-to-1
The following table gives the house edge and standard deviation for each of these wagers in the case when UWE is offered in an eight-deck shoe:
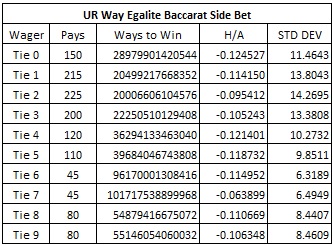
If a player makes equal wagers on each of these 10 bets, then he is essentially playing a “Tie bet” with a wager of 10 units. A simple computation shows that this modified “Tie bet” pays at odds of about 8.83-to-1, making it much better for the player, on average than the ordinary tie bet that pays 8-to-1. This shift towards the player can also be seen by observing that the 8-to-1 Tie bet has a house edge of 14.360%, whereas the wagers listed above have smaller house edges, ranging from 6.49% to 14.27%.
What makes UWE especially vulnerable is that a specialized card counting system can be developed individually for each of these 10 bets. By separating out the ten different totals for a tie into ten different wagers, different card counting systems can be created for each. These card counting systems will target the specific cards that make their individual tie more likely.
The following table gives the EORs for each of the ten UWE tie bets, when UWE is offered from an eight deck shoe:
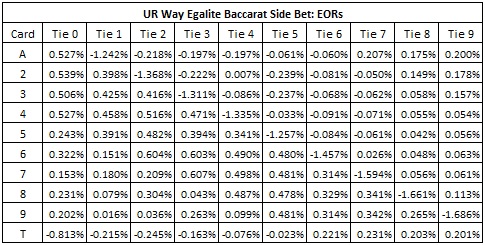
The size of these EORs is surprising. For example, if a single “8” is removed from an eight-deck shoe, the house edge on the “Tie 8” bet increases by 1.661%. On the other hand, if a single “6” is removed from an eight-deck shoe, then the house edge on the “Tie 2” bet moves towards the player side by 0.604%. Intuitively, a six often makes a standing hand (not a total of 2). Also, if a six is drawn by the Player, it can never make a total of 2.
From these EORs, I developed a card counting system for each of these ten wagers. The following table gives these ten different card counting systems. The bottom row gives the “betting efficiency” (B/E). This number gives a measure of how closely these card counting systems line up with the actual EORs: the closer to 1, the stronger the system.
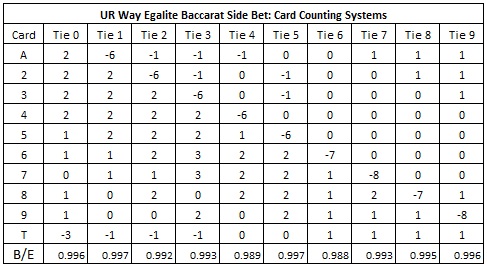
The card counting systems for the Tie 6, 7, 8 and 9 side bets are intuitively clear. For the other tie bets, the drawing rules for baccarat strongly influence the EORs and hence the given card counting systems are more complex.
To test these card counting systems, I ran a simulation for each. The game I simulated has the standard cut card rules:
- The game is dealt from a shoe with eight decks.
- At the start of each shoe, a card is burned. Based on the value of the burn card, an additional number of cards are burned, equal to the value of the card.
- The cut card is placed 14 cards from the end of the shoe.
- After the cut card is dealt, one more round is dealt before shuffling.
The following tables give the results from ten different simulations, each simulation consisting of two hundred million (200,000,000) shoes. Each simulation gives the results of using specified card counting system against its respective tie bet (click on the image to make it larger):
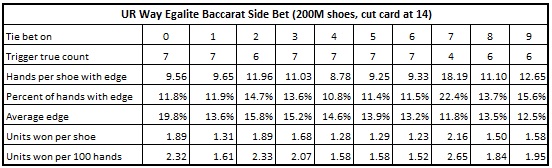
The strongest single opportunity arises by targeting the “Tie 7” UWE side bet. This wager produces an average profit of 2.16 units per shoe or 2.65 units per 100 hands. The AP will have an edge on 22.4% of the hands, and when he makes the “Tie 7” wager, his average edge will be 11.8% over the house. By comparison, the Dragon 7 side bet in EZ Baccarat returns about 0.597 units per shoe. That is, the “Tie 7” side bet from UWE is about four times as profitable for the AP as the Dragon 7 side bet in EZ Baccarat.
However, the combination of these opportunities together gives a unique opportunity. A team can be assembled, each counting one of these ten wagers. Whenever a team member hits his target count to make his particular UWE tie bet, the other team members follow suit, making the tie bet on the same number.
For example, a team of three APs might choose to target the three most profitable UWE tie bets. By considering the table above, these are “Tie 0”, “Tie 2” and “Tie 7.” Each AP will use the particular card counting system given above to count his tie bet. Although these card counting systems may appear to be tough to use, in baccarat using a score card, it would be a triviality. The AP could write his system and cards played on his score card to help keep his count.
The following table gives the units won per shoe for each team member and overall using this team approach:
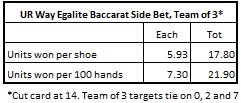
If the maximum wager allows on UWE is $100 on any number, then each AP will earn about $593 per shoe, or about $730 per 100 hands. Altogether, this team of three APs will earn about $1,780 per shoe, or about $2,190 per 100 hands.
A larger team could earn significantly more. In the unlikely (but not impossible) situation where a team of ten APs keep all ten counts, each individual team member would earn about 15.81 units per shoe, and the team overall would earn about 158.1 units per shoe. If each team member wagered $100 on those UWE tie bets that have the edge, as indicated by the team member counting that specific tie bet, then this team overall would earn about $15,810 per shoe, or about $19,450 per 100 hands.
In the literature for this wager, I found the following statement:
If this wager is made available, then the second cutting card must be inserted 14 cards from the other cutting card. If the cutting card is displayed after a completed coup, then the Dealer must announce that was the last coup of the shoe and the cards reshuffled.
My view is that this statement acknowledges the vulnerability of UWE to advantage play. The suggested fix is to place the cut card at 28 cards rather than at 14 cards. By dealing fewer cards per round, card counting is rendered less effective. While that is certainly the case, the vulnerability of UWE to card counting is still significant.
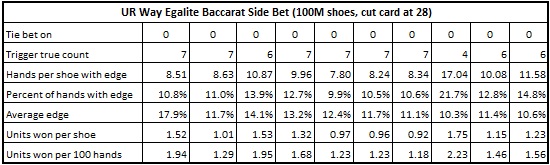
The following tables give the results from ten different simulations, each simulation consisting of one hundred million (100,000,000) shoes with the cut card placed at 28 cards. Each simulation gives the results of using specified card counting system against its respective tie bet:
Once again, a team of three APs will count “Tie 0”, “Tie 2” and “Tie 7.” Each AP will use the particular card counting system to count his tie bet. The following table gives the units won per shoe for each team member and overall using this team approach:
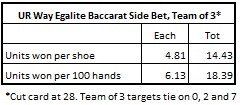
If the maximum wager allows on UWE is $100 on any number, then each AP will earn about $481 per shoe, or about $613 per 100 hands. Altogether, this team of three APs will earn about $1,443 per shoe, or about $1,839 per 100 hands. A team of ten APs can theoretically earn about $12,370 per shoe or about $15,760 per 100 hands.
UWE has an extreme vulnerability to a card counting methodology of advantage play. A solo counter can earn at a rate of about 4-times the earning potential of the Dragon 7. A team of three AP’s can earn $1,443 per shoe at the recommended cut card depth of 28 cards. In an unprotected game, a team of ten AP’s can quickly empty the rack. I recommend that any casino that offers UWE be attuned to its extreme vulnerability to card counting. Especially, watch out for team play.


