The Pairs bet (PB) is a non-proprietary baccarat side bet that pays 11-to-1 for a dealt pair. The player can wager on either or both of the Player or Banker side to be dealt a pair. Unlike the Tie bet which is essentially worthless (see this post and this post), PB is highly vulnerable to advantage play. The fact that PB is found on baccarat tables around the world, often with table limits as high as $10,000 or more, makes it a premium target for advantage play. In this post I am going to give the win-rate statistics against PB using computer-perfect play. I will also give a side-by-side comparison with the Tie bet.
The following table gives the combinatorial analysis for PB for an eight-deck shoe:
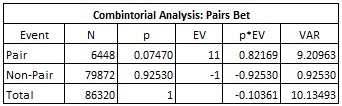
In particular:
- The house edge is 10.361%.
- The hit frequency is 7.470%.
- The standard deviation is 3.184.
To achieve computer-perfect play, I assume the AP is keeping track of the cards that have been played from the shoe. Before the start of each round, the AP uses a computer to give him the exact edge on PB based on the knowing the composition of the cards left in the shoe. If the AP has the edge over the house, he makes a PB wager; otherwise he does not place a wager. These results give an absolute upper bound on the earning potential against the PB through ordinary advantage play.
PB is the rare wager where computer-perfect play can be achieved in practice. The "targets and weights" counting system given in this post is nearly perfect. In addition, some casinos allow high-rollers to “play by phone.” In those cases, the player can use a simple spread sheet to keep track of the edge on PB. Here is a spread sheet that can be used for computer-perfect play:
Finally, in some jurisdictions there are no device laws. In particular, there are smart phone apps that allow the player to track the edge on PB. A player caught using such a device can be kicked out of the casino, but he cannot be prosecuted. He simply hands off his device to a teammate who continues the onslaught. This problem is especially critical in “stadium” baccarat, like the following (image from Google images):

The following picture shows a device built for computer-perfect play against PB:

To continue on, this analysis assumes an eight-deck shoe. We assume the game uses the following standard burn-card and cut-card rules:\
- A card is dealt and exposed at the start of the shoe.
- Based on the value of that card an additional number of unseen cards are burned.
- If a Jack, Queen or King is exposed, then 10 cards are burned, otherwise, the number of burned cards equals to the pip value of the exposed card.
- If the cut-card is dealt mid round, then one additional round is dealt.
- If the cut-card is the first card dealt in a round, then two additional rounds are dealt.
With these rules, the cut-card can be placed no less than 12 cards from the end. If the exposed card is an Ace (so that there is one unseen burned card) and the cut card is set at 12 cards, then it is possible that in the final round, there are only six cards remaining in the shoe (seven unseen cards). If the final round takes six cards, then the shoe will be entirely depleted. I will consider cut-card placements from 12 cards to 26 card (1/2 deck). For game protection consideration, I also give results for cut card placements at 39 cards (3/4 deck), 52 cards (1 deck) and 104 cards (2 decks).
One of the unique opportunities that advantage play against PB gives is the ability to wager on either or both of the Player and Banker starting hands to be pairs. These are separate wagers, each earning at the full win-rate for computer perfect play. The ability to wager on two different hands allows the AP to effectively earn at twice the rate for a fixed maximum bet.
Here are the statistics from simulations of computer-perfect play against the Pairs bet. The statistics given in each column were obtained by a simulation of one hundred million (100,000,000) baccarat shoes using computer-perfect play. The final row gives the units won per 100 hands for the AP who makes both Player and Banker wagers:
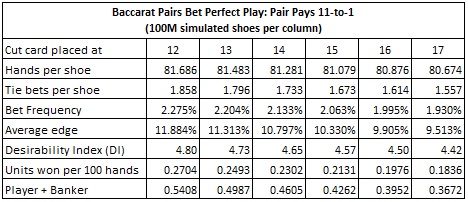
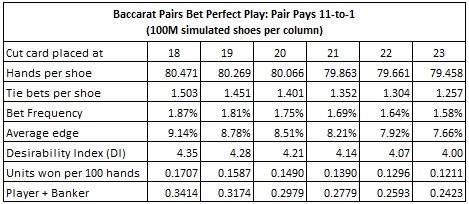
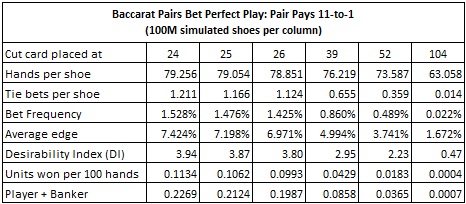
It is worthwhile comparing the results for computer-perfect play against the Pairs bet with computer-perfect play against the Tie bet. The following table gives side-by-side statistics for computer-perfect play against these two bets when the cut-card is placed at the traditional location of 14 cards:
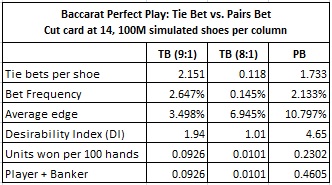
These statistics highlight the striking vulnerability of the Pairs bet. The Tie bet is almost always offered with an 8-to-1 payout. The statistics given in this table show that an AP who makes a $10,000 wager whenever he has the edge will earn approximately $101 per 100 hands playing against the Tie bet, while making $4605 per 100 hands playing against the Pairs bet. In other words, the Pairs bet is a big game protection problem.
The following are my suggestions for safeguarding the Pairs bet from advantage play:
- Increase the cut-card depth to at least 26 cards.
- Do not expose the initial burn cards.
- Watch for players who make PB wagers late in the shoe, who bet on both sides, and who make table maximum wagers.
- Watch for players who keep score in an unusual manner.
- Watch for player who may be using devices in stadium baccarat.
- Watch for “play-by-phone” players who make large PB wagers.


