The use of fear to influence the opinions and actions of others towards some specific end is called “fear mongering.” One of the most infamous cases of using this tactic was Lyndon Johnson’s “Daisy” commercial, which was used it in his 1964 election campaign against Senator Barry Goldwater (watch it here). Fear is also widely used in advertising, where it is sometimes referred to as “shock advertising.” Several advantage players have stated the opinion that I use this blog to create fear in order to drive interest in my consulting services ("...he is making people so scared.” -- Richard Munchkin). Not every daisy is a nuclear bomb. That doesn't mean there are no weapons of mass destruction.
In this post I will give a foundation for evaluating and comparing the risks associated with card counting blackjack side bets. To accomplish this, I am going to use Donald Schlesinger's “desirability index” (DI). Intuitively, DI gives a measurement of the risk-normalized return from an advantage play opportunity. At least, that’s what it intuitively means to me. Here is how Schlesinger defines it in his book “Blackjack Attack” (page 186):
I have christened this ratio the “Desirability Index” (DI) and have defined it, for the play all game, to be equal to one thousand times (for convenience of expression) the ratio of that game’s per-hand win rate to the per-hand standard deviation. Similarly, for the back-counted game, DI = 100 times the ratio of that game’s win rate per 100 hands to the s.d. per 100.
The purpose of the DI is to give a single number by which all card counting opportunities can be compared. This number provides a level playing field. No amount of fear mongering can increase or decrease the value of DI.
The higher the number, the better the game. In general terms, a player would look for a desirability index of 6.6 or higher to find game which would be considered to be playable to most counters.
Although DI was originally intended just for the main game of blackjack, it can be applied to any advantage play opportunity. DI can be used to compare ordinary blackjack card counting to card counting side bets, hole-carding, edge sorting, collusion and any other form of advantage play that can be accurately quantified. It is a one-size-fits-all measurement.
To apply DI to side bets, note that all side bets can be considered to be “back-counted.” This means that they are only played when the AP has the advantage and at no other time. Thus, only the second part of the definition above applies to side bets. It follows that:
DI = 100*(win rate per 100 hands) / (standard deviation per 100 hands)
Let’s look at the two parts of this fraction more closely.
Win rate per 100 hands. This is just the win in units per 100 hands that I give in my analysis of every side bet.
Standard deviation per 100 hands. There is an easy way to approximate this value. Using combinatorial analysis, first obtain the per-hand standard deviation of the side bet for the non-advantage player. This value is then used as an approximation to the standard deviation for the back counting advantage player. Then,
Standard deviation per 100 hands ≈
sqrt(100 x bet frequency) x (standard deviation per hand)
[Math note. Certainly, the standard deviation for the non-advantage player will be different from that of the advantage player. The AP will hit the large payouts slightly more often when he makes a bet. This will tend to slightly increase his standard deviation. On the other hand, the formula for the standard deviation subtracts the edge from the payouts. Because the edge is positive for the AP, the effect of this will be to make the standard deviation slightly smaller. I am going to brashly assume that these two factors roughly cancel each other out.]
With all the ingredients for computing the DI’s at hand, it’s time to compare apples to apples. To begin with, when considering the world’s greatest blackjack player, we get the following DI’s for ordinary blackjack card counting:
- For two decks, with the cut card placed at 75 cards (29 from the end): DI = 9.94.
- For six decks, with the cut card placed at 260 cards (52 from the end): DI = 5.42.
Keep in mind that my analysis assumes a $100 wager when the player has an edge; otherwise the player keeps the count without wagering. In comparing ordinary blackjack to side bets, we are comparing a blackjack card counter with a maximum wager of $100 to a card counting AP making a flat $100 wager on a side bet when he has the edge. With this understanding, I make the following categorization of risk:
- minimal: no meaningful risk to advantage play.
- low: very low risk, card counting is highly unlikely.
- medium: risk is roughly equivalent to ordinary card counting (with the same maximum wager), take equivalent measures.
- high: substantial risk to high-level advantage play, game should be carefully monitored.
- extreme: imminent risk of significant loss to advantage play, take immediate steps to safeguard game.
The following table gives DI’s for all of the two-deck side bets I have considered. In each case, I use the best card counting system available.
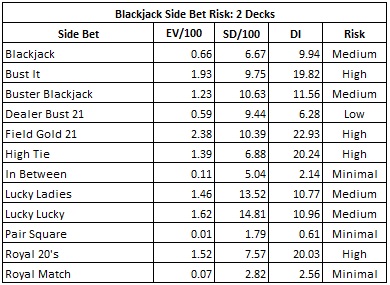
The following side bets are those with a DI less than that of two-deck blackjack:
- Pair Square, DI = 0.61.
- In Between, DI = 2.14.
- Royal Match, DI = 2.56.
- Dealer Bust 21, DI = 6.28.
In particular, the first three are yawners when it comes to advantage play.
Every other side bet listed has a higher value of DI than ordinary two-deck blackjack. But for the fact that the maximum wager on blackjack side bets is typically fairly low, these side bets are significantly more appealing to the advanced AP. In particular, the four side bets with the highest values of DI are:
- Field Gold 21, DI = 22.93.
- High Tie, DI = 20.24.
- Royal 20’s, DI = 20.03.
- Bust It, DI = 19.82.
In my opinion, these four wagers fall into "high risk" territory and should be continuously monitored for advantage play. In particular, Royal 20's allows the player to wager on both the Player and Dealer having a 20, giving two opportunities per hand.
The following table gives DI’s for all of the six-deck side bets I have considered. In each case, I used the best card counting system available.
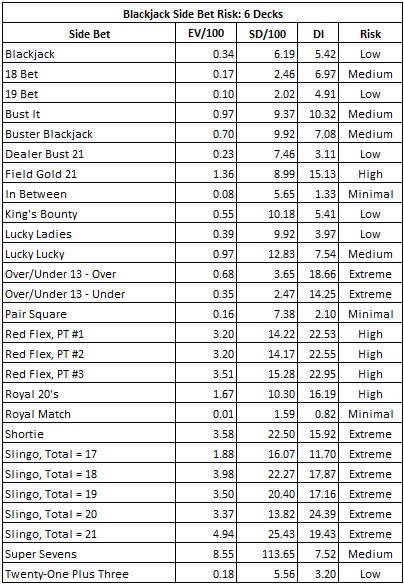
The following side bets are those with a DI less than that of six-deck blackjack.
- Royal Match, DI = 0.82.
- In Between, DI = 1.33.
- Pair Square, DI = 2.10.
- Dealer Bust 21, DI = 3.11.
- Twenty-One Plus Three, DI = 3.20.
- Lucky Ladies, DI = 3.97.
The four side bets with the highest DI’s for six-deck blackjack are:
- Slingo, DI = 11.70 to 24.39.
- Over/Under 13, DI = 14.25, 18.66
- Red Flex, DI = 22.53 to 22.95.
- Shortie, DI = 15.92.
Slingo and Over/Under 13 are in “extreme risk” territory and are at imminent risk to advantage play if offered. Slingo is probably extinct by now; its last sighting in 2012 was hit pretty hard. Likewise, the Over/Under 13 wager is usually offered using a continuous shuffle machine. The remaining two, Red Flex and Field Gold 21, are "high risk" wagers that need to be continuously monitored for advantage play.
By means of DI's we have achieved a level comparison. Look up the DI of the side bets you offer. Use these values to assess your risk. Don’t overreact; you’ve got scarce resources, use them wisely.
I have no intention of using fear to sell my services. I hope the values offered here lay bare the relative risks. There is no reason to equate daisies with nuclear bombs. Fear not.
If The Table Maximum is $25 on a Side Bet
Many casinos do not offer $100 table limits on their side bets. If the table maximum is $25 on a side bet and that is being compared to a $100 perfect blackjack card counter, then the apples-to-apples comparison would require dividing the side bet DI's by 4. In this case, the only wagers that remain at medium and above levels are:
- Slingo, 6 decks: Extreme
- Over/Under 13, 6 decks: High
- Red Flex, 6 decks: Medium
- Royal 20's, 2 decks: Medium
I would also recommend keeping an eye on:
- Field Gold 21, 2 decks and 6 decks
- High Tie, 2 decks
- Bust It, 2 decks
With a $25 table limit, every other side bet is substantially less profitable than a perfect card counter at a six-deck game with a maximum wager of $100. In particular, Lucky Ladies is very low risk to card counting on a six-deck shoe game with a table maximum wager of $25. Stop sweating it.
My opinion is that players should be allowed to place higher wagers if that's what they want to do. The casino is leaving money in the pockets of its customers by not allowing $100 wagers on blackjack side bets. A bit of education will safeguard these wagers, while creating the likelihood of a significant increase in profitability from these side bets.


