Lucky Ladies (LL) is a blackjack side bet that pays for any player 20, with premium payouts for suited or matched 20’s and a top pay for a pair of Queen of Hearts. I covered card counting the Lucky Ladies side bet in this blog post. As noted in that post, any count that distinguishes face from non-face cards will be very effective against LL. A count that I did not consider is the one analyzed in this blog post that is primarily used to target the Insurance (INS) side bet. This post addresses the value of using the INS count to target LL.
The LL side bet pays based on the first two cards dealt to the player. In the event the player is dealt a pair of Queen of Hearts, the dealer’s hand is also evaluated. To review, the following table gives the payouts for LL for various numbers of decks: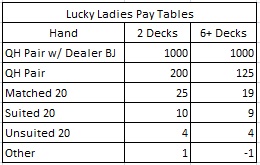
The following table gives the statistics for LL for various numbers of decks: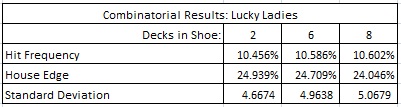
The INS count has the tags (1, 1, 1, 1, 1, 1, 1, 1, 1, -2). Although it is unbalanced, it is perfectly correlated with INS: the counter takes insurance whenever the running count is 4*D + 1 or higher, where D = number of decks. There is no true count conversion necessary when using this count. It gives perfect information as a running count alone.
The following table gives statistics for using the INS count to play against Insurance. Each simulation consisted of one hundred million (100,000,000) shoes.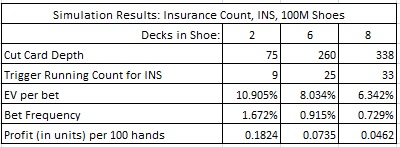
Now suppose that the INS count is used to target LL. Again, we assume that no true count conversion is used. In this case, we are simply concerned with identifying trigger running counts. The AP plays the LL bet when the INS running count is greater than or equal to the trigger count.
The following table gives statistics for using the INS count to play against LL. Each simulation consisted of one hundred million (100,000,000) shoes.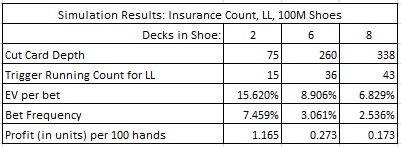
For example, consider a double-deck game with the cut card placed at 75 cards. The AP who uses the INS count against LL will make the LL bet whenever the running count is 15 or higher. In this case, the AP will make the LL bet on about 7.46% of his hands, and will have an average edge of about 15.62% over the house. If the AP is playing heads-up, getting 200 rounds per hour, and is making a $100 wager on LL whenever the count indicates, then this AP will earn about $233.00 per hour playing against the LL wager using the INS count.
There is an implication worthy of note: If the AP is making an LL wager, then the AP will take Insurance if offered. Not taking Insurance implies no LL bet.
The following table compares the INS count for both LL and Insurance with a dedicated LL count used only for LL (no Insurance bets). The second line in this table gives the units won per 100 hands for using the INS count to simultaneously target both Insurance and Lucky Ladies. The third line gives the units won per 100 hands for using a dedicated LL count and playing only against Lucky Ladies.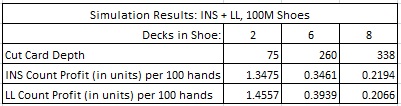
Note that the dedicated LL count performs better than the INS count in both the 2-deck and 6-deck games. However, for an 8-deck shoe game, the INS count performs better.
It has been known for a long time that LL is susceptible to card counting. Few opportunities exist for APs to effectively target this side bet by itself. However, two counters working together on a shoe game can gain a moderate overall edge when one uses an ordinary blackjack card counting system (like High-Low) and the other uses the INS count to target both LL and INS.
The following are my recommendations for protecting against the LL, INS combination:
- Watch for players who play INS and LL together, especially late in the shoe.
- Decreasing penetration has a strong effect in neutralizing AP opportunities.
- Watch for the other tells of an ordinary card counter.


