One of the first games I posted about on this blog was the blackjack side bet Twenty One Plus Three (21+3). In this post, I showed that there was very little possible profit against 21+3, even using perfect play. Nevertheless, this post on card counting 21+3 is the most viewed blackjack side bet article in this blog, getting about 70% more hits than this second place post on Lucky Ladies. The 21+3 post ranks 6th in overall views. It continues to be one of the top posts accessed each day. I don’t know why.
For over two years, I have known about a version of 21+3 called “21+3 Extreme” (21+3E). This version pays for the same events as 21+3, but uses a pay table leading to a higher house edge and greater volatility. Because of the extremely low vulnerability of 21+3 to advantage play and the higher house edge of 21+3E, I long ago concluded that 21+3E would be a waste of time to analyze. However, given the continued interest in 21+3 (and a lack of anything better to do), I decided to finally give 21+3E a look. The results of this analysis met my extraordinarily low expectations.
This post covers the six-deck case. With fewer decks, the house edge for 21+3E increases, making it even less vulnerable.
Both 21+3 and 21+3E pay based on the poker value of the three card poker hand consisting of the player’s first two cards and dealer’s up card. The paying hands are Straight Flush, Three of a Kind, Straight and Flush. In the case of 21+3, each of these pays 9-to-1. In the case of 21+3E, the payout for these events is 30-20-10-5.
The following tables give the combinatorial analysis for 21+3 and 21+3E: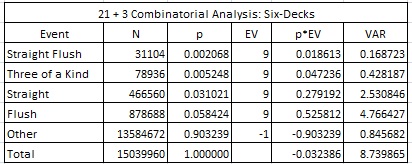
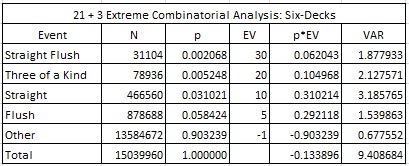
In particular the house edge for 21+3 is 3.24%, whereas the house edge for 21+3E is 13.39%. The term “Extreme” certainly describes this side bet: it is “Extremely” good for the casino and “Extremely” bad for the player.
The following Excel spread sheet allows the user to input the exact composition of the shoe and the pay table for the variation of 21+3 in use; it outputs the house edge, hit frequency and standard deviation. I suppose in some universe a spread sheet like this could be used for advantage play against 21+3. Then again, in some universe, a Komodo dragon is the current world chess champion.
In investigating card counting 21+3E, the AP can do no better than perfect play (for example, by using the spread sheet given above), where the AP makes a wager on 21+3E if and only if he has the edge. The following table shows the results of perfect play against 21+3E in the six-deck case when the cut card is placed at 260 cards. These results confirmed my intuitive expectation that 21+3E has almost no card counting vulnerability: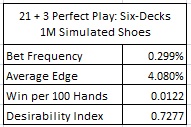
The opportunity to make a 21+3E wager with the edge occurs about 3 times per 1000 hands. When the player makes a 21+3E wager, his average edge is about 4.08%. This leads to a gain of about 0.0122 units per 100 hands. If an AP is making a $100 wager whenever he has the edge over 21+3E, and otherwise does not make a wager, then he will earn about $1.22 per 100 hands.
The final number given in this table, the desirability index (DI), is discussed for blackjack side bets in this post. The value 0.73 given in this table shows that 21+3E has “minimal vulnerability” to advantage play. (I note that I used the standard deviation from the combinatorial analysis for 21+3E in computing the DI).
To get a different view on the vulnerability of 21+3E, I kept track of the average edge and bet frequency by the location in the shoe at the start of each hand. As noted above, I assumed the cut card was placed at 260 cards, so the simulation did not include values beyond that point. I found that there were essentially no advantageous situations before 175 cards were played from the shoe.
The following plot gives perfect-play results by first-card location, based on a simulation of one million (1,000,000) six-deck shoes with the cut card at 260 cards (click for full-sized image).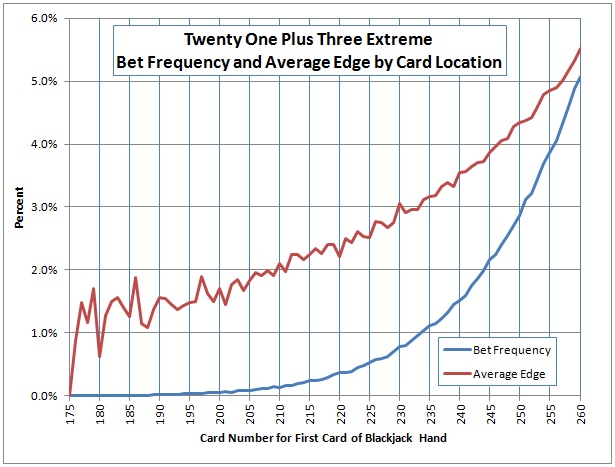
The average edge is jagged to begin with. This occurred because there were very few data points being averaged together. As the depth into the shoe increased, there were more instances of advantageous situations, so the average edge smoothed out. The average edge appears to be increasing in direct proportion to the card location, whereas the bet frequency appears to be increasing quadratically. At exactly the 260 card position, the values that the simulation produced were a bet frequency of 5.08% and an average edge of 5.52%.
My conclusion is that 21+3E has a minimal vulnerability to advantage play. No serious AP is going to give 21+3E a second thought without some other vulnerability at the game. For example, if the shuffle is highly trackable and a slug of cards of the same suit can be followed through the shuffle, then it could be very profitable to play 21+3E during the slug.
My recommendations for game protection for 21+3E are as follows:
- Learn about something else.
- Protect something else.


