- A common question I get from aspiring professional advantage players is how much of a starting bankroll do I need to become a professional advantage player?
- Stated another way, they want to know the minimum amount of a bankroll they need to give them a good chance of success.
- The simplest answer is an infinite bankroll. But since most players don’t have an infinite bankroll we have to find more reasonable answer. However, there is no straight forward answer to this question and its answer is different for each person.
- There are certain things to consider when you are answering this question. In short, it depends on severable variables.
The 3 things you need to to know in order to decide about your bankroll size are:
- Your advantage over the house.Your risk tolerance.
- What betting criteria you are using.
TIP 1: YOUR ADVANTAGE OVER THE HOUSE
The first tip is depends on the particular game you are playing. Determining your advantage a complicated task and varies depending on the type of Advantage Play you are executing. Blackjack is the most common game where an advantage play can be executed but it is not the only game. Roulette, Three Card Poker and to some extent Craps all are beatable if the player is skilled enough.
The theoretical advantage a player obtains is often a result of long hours of thinking and even longer hours of computer programming and simulations. Even a 1% advantage over the house is considered a massive edge. But some plays can yield the player an advantage in the neighborhood of 3%. Anything beyond an advantage of 3% a player requires no more than 75 units. I always caution on being more conservative when determining our advantage. Even the most brilliant AP knows that simulation is always better than the actual execution. There are unknown error factors that are not accounted for in the simulation. Computers are perfect, human play is not.
TIP 2: YOUR RISK TOLERANCE
How much a risk is the player willing to take when trying to beat the casino? For instance, if a player has $10,000 to play with they can bet it all on one roll of the dice or all on one hand of blackjack. The result of this is essentially a coin flip- A 50-50 shot at doubling your bankroll or losing it all on one round of play. Most people see this as too much of a risk. The next option is to take that $10,000 and divide it into two rounds of $5,000 each. This is still very risky because losing two in a row is pretty common. But this is less risky than one hand of $10,000 but still too risky for most players. The point is the more units you divide your initial bankroll into, the less risky your play will be. This is why when you have an infinite bankroll your risk tolerance goes to zero. This is why a casino has an advantage over the player, because they have an infinite bankroll.
The graph below illustrates the relationship between the number of units required given a specific advantage and defined risk tolerance. 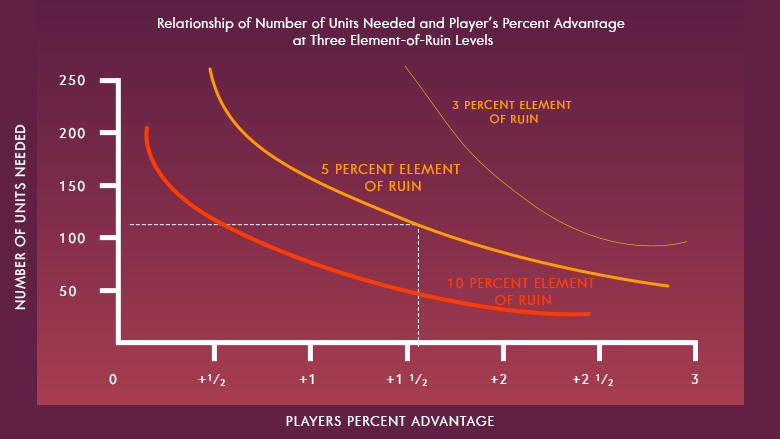
TIP 3: WHAT BETTING CRITERIA YOU ARE USING
The most mathematically centric betting criteria in gaming is the Kelly Betting Criteria. The Kelly Criteria is well known in gambling theory and is a formula used to determine the optimal size of a series of bets. Simply stated the Kelly Bet amount is the optimal bet amount for maximizing the expected bankroll growth while minimizing the risk. The objective for a Kelly betting scheme is to double the bankroll in the minimal amount of time. The full betting Kelly criteria dictates 222 units. Most players play to a fractional Kelly unit of either ½ or 1/3. This is 445 and 667 units respectively. The latter of a 1/3 Kelly unit yields a 98% chance of doubling your bankroll while yielding a 2% chance of a Risk of Ruin; this means you lose your entire bankroll.
The way the Kelly function is set up is it sizes the betting unit the total bankroll. If the player has a $35000 initial bankroll than the betting unit is $50 (rounding up to 700 units for simplicity). But when player has a good session and wins $5000 then the original unit size of $50 is no longer optimal, and they are under betting given the increased bankroll. Similarly if a player takes a hit in a session and loses $5000, the initial betting unit of $50 is again no longer valid. The player is now over betting their bankroll. In either instance the dynamic nature of Kelly betting is logistically impossible to implement. To be precise the player would have to resize their betting unit after every win or loss. To bypass the logistic difficulty a general rule of most players is to resize the betting unit after a predetermined bank roll swing. A 25% or 30% swing in a positive or negative direction justifies a resizing of the unit.
SUMMARY
There is no easy answer to what is the minimum starting bankroll a player needs to become a winning player. Several things come into play. Here we have touched on a few aspects that come into play when making the determination.
Determining your advantage is a complicated task and the player must be confident in their calculations because this is a big part of the equation. Being off by even 0.5% can take a positive game to a negative game. Next is the risk tolerance that a player chooses to adhere to. The higher your risk tolerance the less of a starting a bankroll the player you need.
If the player chooses to go the strict mathematical route the Kelly Criteria is the best route to take. There are resizing considerations that must be taken into account. Adhering to these three things will give the player a good foundation on to determining what their starting bankroll should be.


