The first Wearable Computer was created to predict roulette.
The cigarette pack sized analog device yielded an expected gain of +44% when betting on the most favored “octant” of the wheel. Shannon and Thorp tested the roulette computer in Las Vegas in the summer of 1961. The predictions of the roulette numbers where the ball will land, were consistent and offered a 44% advantage, but a minor hardware problem deferred sustained high stakes betting and winning real money from the casino. This roulette method and the existence of the wearable roulette computer have been kept a secret until 1966.
 |
| The first wearable roulette computer created by Thorp and Shannon in 1961. |
1955: How to win at roulette?
In the spring of 1955 while finishing my second year of graduate physics at U.C.L.A., I thought about whether it was possible to beat the roulette wheel. A theorem said no mathematical system existed. What about biased (defective) wheels? Al Hibbs and Roy Walford had successfully and sensationally exploited one in Reno in 1949-50, but wheels now usually do not have exploitable imperfections. I believed that roulette wheels were mechanically well made and well maintained. With that, the orbiting roulette ball suddenly seemed like a planet in its stately, precise and predictable path.
I set to work with the idea of measuring the position and velocity of the ball and rotor to predict their future paths and from this where the ball would stop.
Such a system requires that bets be placed after the ball and rotor are set in motion. Thus the casinos have a perfect countermeasure: forbid bets after the ball is launched. However, I have checked games throughout the world and rarely were bets forbidden after the ball was launched. A common practice instead was to call “no more bets” a revolution or two before the ball dropped into the center. The simple casino countermeasure meant
that in addition to predicting, one must conceal the system.
For camouflage I planned to have an observer near the wheel recording numbers that came up, as part of a “system.” This is common and doesn’t seem out of place. But the observer would also wear a concealed computer and time the ball and rotor. (Later we used toe-operated switches, leaving both hands free and in the open.) The computer would send the prediction by radio to the bettor who, at the far end of the layout, would appear unrelated to the observer-timer. The bettor would have a poor view of ball and rotor and would not pay much attention to them. To further separate timer and bettor, I would have several of each, with identical devices. They would each come and go “at random.”
A bettor who only bet after the ball was launched, and who consistently won, would soon become suspect. To avoid that, I planned to have the bettor also make bets before the ball was launched. These would be limited so their negative expectation didn’t cancel all the positive expectation of the other bets.
1955-60: Clocking and understanding the roulette wheel
I began work late in 1955. Confident of the idea, I started on the radio link concurrently with physics experiments. Then I studied a cheap half scale wheel by making movies of the wheel in action, and to time each frame the picture included a stopwatch that measured in hundredths of a second. By studying the film and plotting orbits from this data, I learned that my wheel and ball were very irregular and that their defects prevented predictability. But full-sized wheels were not like that. In December 1958, partly to study real casino wheels, I made my trip. I observed several wheels and found that the ball moved smoothly in its track. When I saw how good the casino wheels were, I believed that prediction was possible. But now I needed a full-sized wheel and some good laboratory equipment.
Ironically, on this same trip, I happened to try out a recently published blackjack strategy by Baldwin et al. This led quickly to the idea for a winning blackjack card counting system and I set to work intensely. Then in March or April of 1959, twelve man years of blackjack calculations arrived, courtesy of Baldwin et al and I put the roulette project aside.
In the summer of 1959 I moved from U.C.L.A. to M.I.T. where I wrote my blackjack computer programs. By mid 1960 I had the basic results for the five-count system, most of the ten-count system and the ultimate strategy. I also worked out the methodology leading to today’s “one parameter” blackjack systems. Fear of plagiarism and worse (fulfilled) led me to seek quick publication. I chose the Proceedings of the National Academy of Sciences. Needing a member of the Academy to communicate my paper, I sought out the only mathematics member at M.I.T., Claude Shannon.
I arranged an appointment early one chilly November afternoon. But the secretary warned me that Shannon was only going to be in for a few minutes, not to expect more, and that he didn’t spend time on subjects (or people) that didn’t interest him.
Feeling awed and lucky, I arrived at Shannon’s office to find a thinnish alert man of middle height and build, somewhat sharp featured. His eyes had a genial crinkle and the brows suggested puckish incisive humor. I told the blackjack story briefly and showed him my paper.
Shannon was impressed with the results and method and cross-examined me in detail, both to understand and to find possible flaws. When my few minutes were up, he pointed out in closing that I appeared to have made the big theoretical breakthrough on the subject and that what remained to be discovered would be more in the way of details and elaboration. We changed the title from “A Winning Strategy for Blackjack” to “A Favorable Strategy for Twenty-One” (more sedate and respectable). I reluctantly accepted some suggestions for condensation, and we agreed that I’d send him the retyped revision right away to forward to the Academy. And then he asked, “Are you working on anything else in the gambling area?” I decided to spill my other big secret and told him about roulette. Ideas about the project flew between us. Several exciting hours later, as the wintery sky turned dusky, we finally broke off with plans to meet again on roulette.
The winning team: Edward Thorp and Claude Shannon
Shannon lived in a huge old three story wooden house once owned by Jane Addams on one of the Mystic Lakes, several miles from Cambridge. His basement was a gadgeteer’s paradise. It had perhaps a hundred thousand dollars (about six hundred thousand 1998 dollars) worth of electronic, electrical and mechanical items. There were hundreds of mechanical and electrical categories, such as motors, transistors, switches, pulleys, gears, condensers, transformers, and on and on. As a boy science was my playground and I spent much of my time building and experimenting in electronics, physics and chemistry, and now I had met the ultimate gadgeteer.
Our work continued there. We ordered a regulation roulette wheel from Reno for $1,500 and assembled other equipment including a strobe light and a large clock with a second hand that made one revolution per second. The dial was divided into hundredths of a second and finer time divisions could be estimated closely. We set up shop in “the billiard room,” where a massive old dusty slate billiard table made a perfect solid platform for the roulette wheel.
Analyzing the motion of the wheel
The plan was to divide the various motions of ball and rotor into the following simpler stages and analyze each separately:
- The croupier launched the ball. It orbits on a horizontally oriented circular track on the stator, slowing until it falls from this (sloped) track towards the center rotor. Assume first that (a) the wheel is perfectly level, and (b), the velocity of the ball determines how many revolutions it has left before falling off. Then the time for one revolution of the ball would determine how many revolutions and how much time remained until the ball left the track.
- Next analyze the ball orbit from the time the ball leaves the track until it crosses from the stator to the rotor. If the wheel is perfectly level and there are no obstacles, then it seems plausible that this would always take the same amount of time. (We later learned that wheels are often significantly tilted. This tilt can affect the analysis substantially. We eventually learned how to use it to our advantage.)
- There are, however, vanes, obstacles, or deflectors on this portion of the wheel. The size, number, and arrangement vary from wheel to wheel. On average, perhaps half the time these have a significant effect on the ball.
- Assume the rotor is stationary (not true), and predict that situation first. Even a stationary rotor introduces uncertainty due to the ball being “spattered” either backward or forward by the frets (the dividers between the numbered pockets). Thus successful physical prediction can at best forecast with an advantage a sector where the ball will stop.
- Next, assume the rotor is spinning. The ball and rotor are spun in opposite directions increasing their relative velocity. This increases the number of relative revolutions and “stretches” the forecast probability distribution, decreasing predictability. A moving rotor also increases “spattering.” On a given spin, friction slows the rotor very gradually, so one can accurately predict its position when the ball leaves the track.
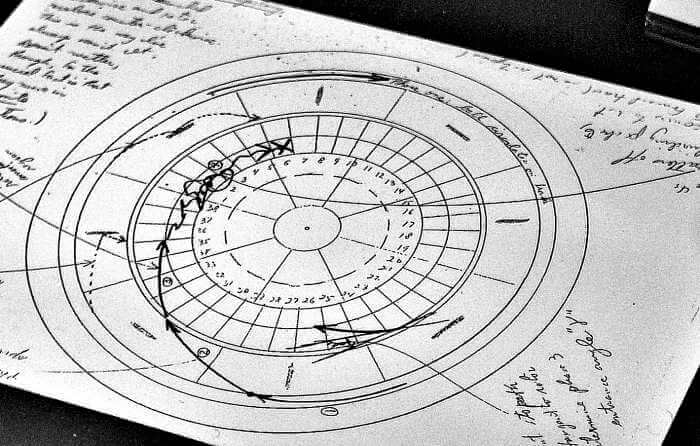 |
| Roulette wheel handwritten movement analysis and calculations |
Timing errors of the computer
First, consider the ball moving on the track. To predict when and where on the stator the ball would leave the track, we timed one ball revolution. If the time were “short,” the ball was “fast” and had a longer way to go. If the time were “long,” the ball was “slow” and would fall from the track sooner. We hit a micro-switch and started the electronic clock as the ball passed a reference mark on the stator. (Actual casino wheels have many such marks.) When the ball passed the reference mark again we hit the switch, stopping the clock and noting the time for this revolution.
The clock switch also flashed a strobe, which “stopped” the ball each time the switch was hit. This showed how much the ball missed the reference mark. Since we knew the ball velocity, we could tell about how much we were early or late in hitting the switch. This let us correct times recorded on the clock, making the data much more accurate. The visual feedback also trained us to become much better at timing.
With practice our timing errors fell from r.m.s. values of about 0.03 seconds to about 0.01 seconds. Later we trained our big toes to operate switches in our shoes and do almost as well.
The total prediction error comes not only from timing but from approximating the complex dynamics of the system, from the “spattering” of the ball on the rotor pocket dividers (frets), the deflection of the ball by metal obstacles as it spirals down the stator, and the possible tilt of the wheel. Assuming the total error was approximately normally distributed, we needed a standard derivation of about 16 pockets (± 0.42 revolutions) or less to get positive expectation both for best single number and best octant bets. We actually achieved an expectation of about 44% for the best single number and about 43% for the best octant, corresponding to a standard derivation of about 10 pockets or ± 0.26 revolutions.
A time of fun and ferment at the casino
We worked from November 1960 to June of 1961 designing and building the computer. Shannon was a treasury of intriguing information and ingenious ideas. In discussing the need for secrecy he mentioned that social network theorists studying the spread of rumors claimed that two people chosen at random in, say, the United States are usually linked by three or fewer acquaintances or “three degrees of separation.” I tested this then and later, with several remarkable confirmations. A June 1998 New York Times Science Times article attributed the degrees of separation idea to a sociologist in 1967. Yet it was well known to Shannon in 1960.
For bet sizing in favorable games, Shannon suggested I look at a 1956 paper by Kelly [3]. I did and adapted it as our guide for blackjack and roulette, and used it later in other favorable games, sports betting, and the stock market [9, 13]. The principle was to bet to maximize the expected value of the logarithm of wealth. This has desirable properties that are discussed in detail in the references.
The Kelly strategy traded a little expectation for a large reduction in risk by diversifying over several (good) numbers. From this and Shannon’s observation that in stimulus – response experiments with n choices (e.g. see a light or hear a tone and then make one of n choices) the response time seems to follow the rule a+b ln n, we settled on “octants.”
As we worked and during breaks, Shannon was an endless source of playful ingenuity and entertainment. He taught me to juggle three balls (in the ′70’s he proved “Shannon’s juggling theorem”) and he rode a unicycle on a “tightrope,” which was a steel cable about 40 feet long strung between two tree stumps. He later reached his goal, which was to juggle the balls while riding the unicycle on the tightrope. Gadgets and “toys” were everywhere. He had a mechanical coin tosser which could be set to flip the coin through a set number of revolutions, producing a head or tail according to the setting. As a joke, he built a mechanical finger in the kitchen which was connected to the basement lab. A pull on the cable curled the finger in a summons. Claude also had a swing about 35 feet long attached to a huge tree, on a slope. We started the swing from uphill and the downhill end of the arc could be as much as 15 or 20 feet above the ground.
Claude’s neighbors on the Mystic lake were occasionally astounded to see a figure “walking on the water.” It was me using a pair of Claude’s huge styrofoam “shoes” designed just for this.
One day I walked into his study to find a cryptic 211=2048 on the blackboard. He had been buying hot IPOs in a raging up-market and doubling his money monthly. He also had been profiting greatly from insightful early stock purchases in local high tech companies.
Shannon seemed to think with “ideas” more than with words or formulas. A new problem was like a sculptor’s block of stone and Shannon’s ideas chiseled away the obstacles until an approximate solution emerged like an image, which he proceeded to refine as desired with more ideas. It was Shannon’s remarkable mind that impressed me most.
1961: Design and construction of the roulette computer
Consideration of a wide range of designs led us to a final version of the computer which had twelve transistors and was the size of a pack of cigarettes. Our big toes input data with microswitches in our shoes. One switch initialized the computer and the other timed the rotor and the ball. Once the rotor was timed, the computer transmitted a musical scale whose eight tones marked the rotor octants passing the reference mark. The computer was “set” earlier to match the wheel and ball and to optimize prediction for a selected number of ball revolutions to go. We usually chose the range between 3 and 4 revolutions. When the timing switch was first hit for the ball, the tone sequence shifted and played faster. As the timing switch clocked the ball for the second time, the tones stopped and the last tone heard named the octant on which to bet. If the timer misjudged the number of ball revolutions left, the tones continued indicating no prediction. Since the prediction, if sent, was simultaneous with the last input, the compute time was zero.
We each heard the musical output through a tiny loudspeaker in one ear canal. We painted the wires connecting the computer and the speaker to match our skin and hair and affixed them with “spirit gum.” The wires were the diameter of a hair to make them inconspicuous but even the hair thin steel wire we used was fragile. The first time I was fully wired up for a rehearsal in the lab, Shannon cocked his head and with a twinkle in his eyes asked, “What makes you tick?”
In April of 1961 I went to Nevada with Mr. X and Mr. Y and successfully tested my blackjack system. I also observed roulette wheels secretly and confirmed that they behaved like our lab wheel. Further, many of them were tilted, a feature which could further improve prediction.
1961: Betting with the computer in Las Vegas
The wearable version of the computer was complete and operational in June of 1961. In the summer of 1961 the Shannons and Thorps met in Las Vegas for a casino test. We used ten cent chips and often turned a few dimes into a pile as yet another octant “hit.” When the computer was working, it worked very well.
Claude generally stood by the wheel and timed, and for camouflage recorded numbers like just another “system” player. I placed bets at the far end of the layout where I paid little attention to the ball and rotor. We acted unacquainted. The wives monitored the operation, checking to see whether the casino suspected anything and if we were inconspicuous. Once a lady next to me looked over in horror. I left the table quickly and discovered the speaker peering from my ear canal like an alien insect.
Claude and Betty and my wife Vivian were nervous whereas I wasn’t, perhaps because my blackjack trip familiarized me with the scene. In retrospect they were right, judging from the Mafia riddled “gaming” industry of the time, accurately shown in the recent movie “Casino.”
The wires to the speaker broke often, leading to tedious repairs and the need to rewire ourselves. This stopped us from serious betting on this trip. Except for the wire problem, the computer was a success. We could solve this with larger wires and by growing hair to cover our ears, a conspicuous style at the time, or persuade our reluctant wives to “wire up.” We adjourned to consider.
1962-98: What is next
An attractive offer took me from M.I.T. in June of 1961 and for reasons such as the difficulties of working together at a distance and the opportunity cost from our other activities, we never continued the project. In 1961 I also built a “knockoff” to predict the “wheel of fortune” or “money wheel” [4]. It used the toe switch for input, the speaker for output, a single unijunction transistor and required only one person. The matchbox sized computer had an expected gain of more than 200% in the casinos but the game had too little action to conceal the late bets and the spectacular consequences.
Finally in 1966, I publicly announced our roulette system because it was clear now that we weren’t going to exploit it. Around 1969 a member of the future Eudaemonic Pie group called and I outlined our work and results in detail. They went on to build an operational wearable roulette computer in the ′70’s using the next generation of technology. They also reported a 44% positive expectation but were ultimately frustrated by hardware difficulties. Other groups also launched secret roulette projects, several of which (including the “Romeo Project”) reportedly led to substantial casino wins.
Shannon and I discussed building a simple wearable blackjack computer but I found mental card counting easier so we passed. However, Keith Taft and others built and marketed them. Finally on May 30, 1985 the Nevada devices law was signed into law as an emergency measure. The target was blackjack and roulette devices. The law banned use or possession of any device to predict outcomes, analyze probabilities of occurrence, analyze strategy for playing or betting, and keeping track of cards played. The descendants of the first wearable computer were formidable enough to be outlawed.
Credits: Edward O. Thorp


