Over/Under (O/U) is a new table game that has recently been approved and is starting to get domestic placements. There has been considerable discussion on advantage play message boards about card counting this game and an associated side bet (see this thread at wizardofvegas.com and this thread at blackjacktheforum.com). In this post, I examined card counting the "Bonus" side bet that accompanies this game. In the present post, I am going to cover card counting the main game and also discuss a two-person team approach to playing against the main game and the Bonus side bet.
According to the available documentation provided by the game's inventor (Joseph Shipman's Report and Donald Catlin's Report), the game of O/U is dealt from a shoe consisting of four, six or eight decks of ordinary playing cards. The game is based on the total value of those three cards, where:
- 2, 3, 4, 5, 6, 7, 8, 9, 10 count as their pip value.
- Jack, Queen and King have a value of 10.
- Ace has a value of 11.
In other words, the total of the three cards is computed in the same fashion as in blackjack, except that Aces always count 11.
To play O/U, the player begins by making a one unit Ante bet. He is then dealt one card, face up. After examining that card, the player has three choices. He can fold, he can make an Over bet, or he can make an Under bet. If made, the Over bet or Under bet must be equal to the Ante bet.
If the player folds then he forfeits his Ante bet and no more action takes place on the hand. Otherwise, the player is dealt two more cards. The player then totals his three cards, as described above. The hand is resolved as follows:
If the player made the Over bet, then:
- If the total of his three cards is 24 or higher, then the player wins and is paid even money on his Ante and Over wagers.
- If the total of his three cards is 23 or less, then the player loses his Ante and Over wagers.
If the player made the Under bet, then:
- If the total of his three cards is 17 or lower, then the player wins and is paid even money on his Ante and Under wagers.
- If the total of his three cards is 18 or higher, then the player loses his Ante and Under wagers.
The player's strategy is based on one piece of information - the rank of his first card. It is clear that if the rank of that card is sufficiently high then he will want to make the Over bet and if it is sufficiently low then he will want to make the Under bet. What isn't clear is if the player should ever fold.
The following table gives the combinatorial analysis for Over/Under along with the expected value for each possible strategy: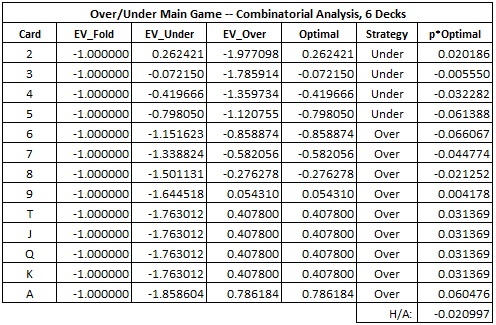
In particular, the house edge for Over/Under is 2.0997%.
Note that the strategy is extremely simple. If the rank of the first card the player is dealt is a 2, 3, 4 or 5, then the player should make the Under bet. If the rank of the first card is 6 or higher, then the player should make the Over bet. The player should never fold.
Because the player never folds, it may be tempting to say that the player will always wager 2 units, and therefore the house edge is half of 2.0997%. In other words, a misunderstanding of the term "house edge" would lead to the statement that the edge is 1.0498%. That is simply not true. This game does not require a 2 unit initial wager; it requires a 1 unit wager. Therefore, the house edge should be based on that wager alone.
It should be intuitively obvious that this game can be card counted. What is not immediately obvious is if both the Under and Over bets should be separately considered. Looking at the table above, note that only the 2 gives a positive EV for the Under bet. Going the other way, the 9, Ten, Jack, Queen, King and Ace all give positive EV for the Over bet. In simple terms, the Over bet is where the lion's share of the player's return comes from. There may be a few pennies to be earned from card counting the Under bet, but I'm not going to deal with that here.
To make this analysis even easier, I am going to assume that the card counter never changes his playing strategy. No matter the count, he is always going to make the Over bet with a 6 or higher and the Under bet with a 2, 3, 4 or 5. The counter will never fold. The only thing the counter will change with the count will be the size of his wager. With this assumption, the following table gives the effect of removal (EOR) for each card, along with a card counting system based on these EORs: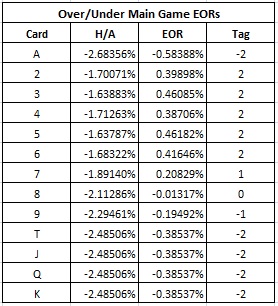
The recommended card counting system has tags:
- 2, 3, 4, 5, 6 = 2
- 7 = 1
- 8 = 0
- 9 = -1
- A, T, J, Q, K = -2
This is a straight-forward balanced card counting system. It has betting correlation 0.990 which is quite strong. This card counting system puts a premium on the cards that give winning Over hands, while penalizing the cards that are likely to give winning Under hands. Essentially, the "Under" side of Over/Under is being completely disregarded by this system.
The following table gives the results of a simulation of one hundred million (100,000,000) six-deck shoes, with the cut card placed at 260 cards, where the player used the card counting system given above. I assumed the player always made an Over bet with a 6 or higher, and an under bet with a 5 or lower: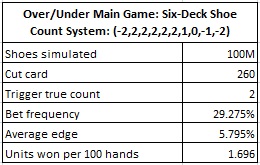
In particular, note that the card counter has the edge when the true count is +2.
The win-rate given in this table may be misleading. Typically I analyze card counting in the context of side bets, when the player does not need to play the side bet every hand. In this game, the player may not be able to "Wong" in and out of the shoe at any given point, only making bets when he has the edge. He may have to play hands where the house has the edge. It is therefore reasonable to consider his win rate when he plays every hand. To do this, we have to account for the average edge the casino has whenever the true count is less than +2.
Here are the values when the house is beating the player (true count less than +2):
- The true count is less than +2 on 70.725% of the hands.
- On average, when the true count is less than +2, the house has an edge of 5.367% over the player.
To see how this fits together, I am going to present a realistic example. Suppose that Over/Under is being played at a casino where the table minimum is $5 and the table maximum is $100. The counter may decide that he wants to "spread" 10-to-1 with a $100 maximum bet. To do this, the counter wagers $10 whenever the count is less than +1, and he wagers $100 when the count is +1 or higher.
Then, out of every 100 hands, on average:
- The player wagers $10 on 70.725 of the hands, with a house edge of 5.367%. In this way, he loses on average $10*70.725*5.367% = $37.96.
- The player wagers $100 on 29.275 of the hands, with a player edge of 5.795%. In this way, he wins on average $100*29.275*5.795% = $169.64.
In other words, the counter loses $37.96 per 100 hands from his $10 bets and wins $169.64 per 100 hands from his $100 bets. Subtracting these, the counter's overall result is to win $131.68 per 100 hands.
By comparison, an average blackjack player using ordinary card counting against a six-deck shoe who has a $100 maximum bet will win about $22 per 100 hands (see this post). Simply put, for the $100 maximum bet player, card counting Over/Under will be nearly six times as profitable as card counting ordinary blackjack.
This can become even more lucrative if two card counters play together. Again, assume a $100 table maximum bet on the Over/Under main game. Additionally, assume a $25 maximum bet on the Over/Under Bonus bet (see this post). One of the card counters (call him "Joe") will keep the Over/Under count described above. The other counter (call him "Fred") will keep the Bonus bet count. When Joe makes a $100 main game wager, then Fred will follow suit and also make a $100 main game wager. When Fred makes a $25 wager on the Bonus bet, then Joe will follow suit and also make a $25 Bonus bet wager. In this way, both Joe and Fred get the full win-rate from counting both wagers.
The following table summarizes the discussion above: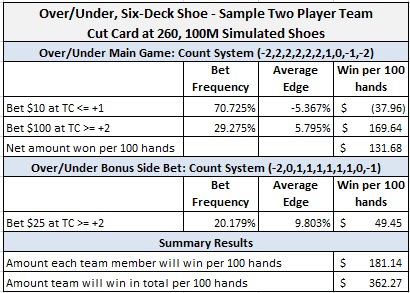
This analysis does not consider a myriad of other possible configurations of the game, including the number of decks used, cut card locations, table maximums and bet spreads. Different count systems could be explored. Maybe a piece of the Under bet could be picked off with a side count. Maybe there is a "strategy" index for the Over/Under decision. Maybe the main bet and Bonus bet can be co-counted using a single count. All of this can be done, of course, but the example above should suffice to make the point.
In my opinion, Over/Under has a serious card counting vulnerability. Any casino that offers it should pay attention to the possibility of card counting either the main game, the Bonus side bet, or team play against both. The easiest fix would be to only deal Over/Under from a CSM. That is my earnest recommendation.


