This post concerns significant errors in the article “Examining a Gambler’s Claims: Probabilistic Fact-Checking and Don Johnson’s Extraordinary Blackjack Winning Streak,” written by W.J. Hurley, Jack Brimberg and Richard Kohar [HBK]. This article appeared in the February, 2014 issue of CHANCE magazine, Vol. 27, No. 1, pages 31-37. Two of the authors, Hurley and Brimberg, are professors in the Department of Mathematics and Computer Science at the Royal Military College of Canada. The third author, Kohar, is a graduate student in the same department.
I discovered HBK while doing a routine Google search on Don Johnson. An online version of HBK can be found here, but you need to be a member of the American Statistical Association (ASA) to view it. As I am not a member of the ASA, I wrote to the authors requesting a copy. The authors kindly and quickly forwarded a pdf copy of their article to me. For the record, I wrote to an editor at CHANCE magazine and asked if I could re-post my pdf copy with this article; my request was declined.
Here are the authors’ opening paragraphs. They come out swinging:
Most gamblers don’t err on the low side when they answer questions about how much they won the night before. In this note, we examine claims about the exploits of a gambler, Donald Johnson (a.k.a. the “Beast of Blackjack”), at casinos in Atlantic City as reported in the popular press …
… Most of these premier periodicals maintain a fact-checking department, where the claims of authors are verified. However, we’re not sure these efforts extend to claims of a probabilistic nature.
In particular, the authors single out these two articles:
- “Meet the blackjack player who beat the Trop for $6 million, Borgata for $5 million and Caesars for $4 million,” by Donald Wittkowski, Press of Atlantic City, May 23, 2011 (article here).
- “The Man Who Broke Atlantic City,” by Mark Bowden, that appeared in The Atlantic, February 27, 2012 (article here).
In their CHANCE magazine article, the authors are stating their shared opinion that Donald Johnson (DJ) exaggerated his winnings, that Donald Wittkowski and Mark Bowden failed to double-check DJ’s claims, and that both The Atlantic and the Press of Atlantic City failed to do their due diligence when it came to fact-checking their authors’ work.
In case there is any doubt that these are the conclusions the authors intended, the final paragraphs of HBK read, in part:
Our purpose was to check statistically whether DJ could have won what the two articles report he won. Our finding is that it was highly unlikely … In the end, it is likely the case that his net winnings over the five month period were overstated.
While ordinary gamblers often exaggerate their wins, when it comes to beating casinos out of millions lots of people are watching. There is plenty of double checking going on. It’s not only DJ doing the reporting of the amount, it’s also surveillance, security, finance, table games and upper management. The casinos in Atlantic City got hit by the amount that DJ stated. This fact has never before been in dispute. Yet, the amount DJ won is precisely what the authors appear to be disputing.
The authors based their conclusions on a calculation that allowed them to estimate the amount that DJ could expect to win each day playing against the loss rebate program he was offered. This amount is called the average daily theoretical win (ADT). To determine DJ’s ADT, the authors used a statistical method called a Monte Carlo simulation. The authors then multiplied DJ’s ADT by the number of days DJ played to estimate the overall amount that DJ should have won for the duration of his play. The authors also estimated DJ’s overall standard deviation for the duration of his play. This allowed the authors to arrive at the rough likelihood that the claims DJ made were accurate.
As a reminder, here are the parameters of the loss rebate deal DJ was offered:
- DJ placed at least $1,000,000 in credit with the casino.
- Any time DJ lost $500,000 or more in a day, he could stop playing and receive a 20% rebate on his loss.
- DJ could place a maximum wager up to $100,000.
- DJ’s rebate reset each day.
Here is the strategy by which DJ achieves his highest possible ADT. These results were obtained by Monte Carlo simulation, as presented in this post. I later confirmed these results by an application of the Second Loss Rebate Theorem, as presented in this post.
- DJ should stop playing after winning 2.4M (quit-win).
- DJ should stop playing after losing 2.6M (quit-loss).
- With these quit points, DJ has an ADT of about $125,000.
- On average, it will take DJ about 480 hands to hit a quit point.
- DJ will hit his quit-win point (leave a winner) on about 49.1% of the days he plays.
The following paragraph summarizes the ADT the authors obtained for DJ by means of their Monte Carlo simulation:
Our analysis suggests that, over a night of blackjack play at the terms he negotiated, DJ had an edge. In particular, we showed that the 20% discount was the term that made the difference. Effectively, this discount translated a negative expected value (-$47,398) into a positive expected value ($41,214).
In other words, the authors concluded that DJ had an ADT of $41,214. The authors then considered overall play periods ranging from 40 to 80 days of total play. Playing 40 days, DJ should expect to win about 40 x $41k = 1.64M. Playing 80 days, DJ should expect to win about 80 x $41k = 3.28M. No wonder the authors disputed DJ’s claims.
In rejecting DJ’s claim that he won 15M in total and had individual winning days in the amounts of 5.8M and 2.25M, the authors stated,
Effectively, we had DJ playing for 100,000 consecutive five-month periods (in total, about 40 millennia) and we didn’t observe the event happening once. To put it into perspective, we would be much more likely to see Joe Di Maggio’s hitting streak broken.
The gap between the authors’ ADT of $41k and my ADT of $125k is huge. It does not take long to find out where the authors begin to go wrong.
The authors’ first significant error was with their model of blackjack. The actual game DJ played was 6D, DOA, DAS, S17, RSA, LSR with a house edge of 0.263% and a standard deviation of 1.142. Including splits, doubles and surrenders, a single round of blackjack would yield a result between winning 8 units and losing 8 units.
In their Monte Carlo simulation, the authors used the following overly simplistic blackjack model that only includes outcomes of +1.5, +1, 0 and -1. Here is the distribution they give:
- The hand ties with probability 0.0982.
- The player gets blackjack with probability 0.0483.
- The player wins 1 unit with probability 0.389275.
- The player loses 1 unit with probability 0.464225.
(Note that in the six-deck blackjack game that DJ played, the probability that the player has blackjack while the dealer does not have blackjack is 0.0453, not 0.0483).
Here is the combinatorial analysis of the authors’ blackjack model:
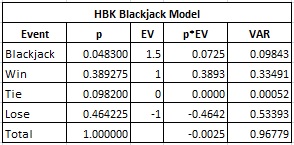
In particular, the house edge in their model is 0.25%. That’s fairly close to the game DJ played, which had a house edge of 0.263%. The problem is that the standard deviation of their model is 0.984. The actual standard deviation of the blackjack game that DJ played is 1.142. The value of a loss rebate promotion to an advantage player is directly proportional to the variance of the game. It follows that the low-volatility blackjack model used in HBK was a significant cause of the authors’ low ADT. In other words, by using a model with the correct standard deviation (and house edge = 0.25%), the authors would have arrived at an ADT of:
New-ADT = (1.142/0.984)^2 x $41,214 = $55,512
This simple fix represents an increase of almost 35% in the ADT they computed for DJ.
On page 32, the authors stated:
We have not modeled some standard blackjack betting outcomes explicitly, outcomes such as splitting pairs, which can be favorable to the gambler. These situations occur so infrequently, they can be ignored without materially affecting the results described herein.
Doubling and splitting are not infrequent occurrences. Any model of blackjack has to include these events. This post contains distributions that can be used to create probabilistic blackjack models for a variety of blackjack rule sets. Appendix 4 at WizardOfOdds.com contains the distribution for the game DJ played.
The majority of the authors’ underestimation of DJ’s ADT came from the quit points the authors used in their Monte Carlo simulation. The authors state that they made the following assumptions when they simulated one night’s play.
- DJ wagered $100,000 per hand over 720 hands.
- The casino refunds 20% of a nightly loss of $500,000 or more.
- The game of blackjack DJ played had a house edge of 0.25%.
- DJ quit playing whenever he lost $500,000 (his quit-loss point was $500,000).
The authors used a quit-loss point of $500,000. They did not use a quit-win point. Instead, they used a time bank of 720 hands. A time bank is a weak strategy against a loss rebate because the longer a player plays the more likely he is to lose. Indeed, the authors determined that DJ would end with a net loss on about 85% of the days he played when using a time bank of 720 hands. Conversely, a player who gets well ahead is unlikely to qualify for the loss rebate before his time bank expires; it follows that he is essentially playing without a discount towards the end of his time bank.
The time bank quit point of 720 hands used in HBK is based on an anecdote by DJ about one specific day in particular when he played 12 hours. No reasonable inference can be drawn that DJ began each day with the intention of spending 12 hours (@ 60 hands per hour) playing blackjack. Nevertheless, the authors have made this boundary condition a fixed part of their model.
The authors used their 85% loss-rate number as an opportunity to take another shot,
Our results indicate there is approximately an 85% probability that our gambler will reach his stop loss before the end of each night. This means that, over a long series of nights doing this same thing, he will lose at least $500,000 on roughly 85% of those nights. We’re not sure Bowden’s characterization, “…although he acknowledge incurring some undisclosed long losses along the way,” is accurate give that, on average, we would expect to see roughly 0.85 x 40 = 34 nights of losses over 40 nights. Surely “many” would have a better word than “some.”
In fact, using optimal quit-win/loss strategy (quit-win = $2.4M, quit-loss = $2.6M), DJ will walk away a winner on about 49% of his nights, so that over the course of 40 nights he should see, on average, roughly 0.51 x 40 = 20 nights of losses. Bowden’s language is just fine as it is.
DJ was no slouch when he designed his strategy to attack Atlantic City. His well-research quit points varied by the maximum wagers he was allowed to make ($50,000, $100,000 or 3x$25,000). Along with these quit points, DJ used table conditions (e.g. dealers who were error prone) to determine when to leave for the day.
There are other sources of positive expected value that the authors did not consider. In addition to DJ’s ADT of $125k from his loss rebate strategy, DJ was also given $50k per day in “show up money.” He also claimed to work hard to create conditions where the dealers made errors. When I heard DJ speak at the World Game Protection Conference in Las Vegas in 2013, he stated that he coaxed about two or three errors per day from the dealers. That’s at least another $200k per day, on average. These additional sources yield about an ADT of at least $375k per day. If DJ played a total of 40 days, then DJ’s expected overall win was 40 x $375k = 15M. This is extraordinarily close to DJ’s claimed win amount.
It is also because of these extra sources of expected value that DJ had some wild volatility. Great opportunities don't persist. Attempting to explain individual winning days of $5.8M and 2.25M with simple win/loss-quit point strategies will lead to huge improbabilities. The authors of HBK considered and dismissed ordinary card counting. Reading between the lines, the authors of HBK should have considered more advantageous methods of play that lie beyond card counting.
On the subject of computer programming, the "pseudo-code" the authors presented in their article indicates that they got their results by averaging together 500,000 “Donald Johnsons.” Why only 500,000? Did the authors write their code in Visual Basic? Did they not have access to high-speed computers? Were they simply impatient? The number of “Donald Johnsons” simulated by the authors is simply not sufficient for them to give results that are accurate to five significant digits (as in their claim that DJ’s ADT was $41,214).
I double checked the authors' Monte Carlo simulation. I duplicated their program, including using their simplistic model for blackjack. I used stopping points of losing $500,000 or playing 720 hands, whichever came first. I then ran one hundred million (100,000,000) "Donald Johnsons." I timed my program, it took 341 seconds to complete. My simulation of their model gave an ADT of $40,429 and showed that DJ would lose on about 85.50% of the days he played. His average number of hands played per day was 192.86. This simulation showed DJ with an effective long-term edge over the house of 0.210% (total amount won divided by total wagers placed).
In summary, the authors:
- Did not use an accurate blackjack model.
- Used sub-optimal quit points.
- Did not consider other ways that DJ gained expected value.
- Only simulated 500,000 DJs, giving unreliable simulation results.
The authors stated,
… as we have demonstrated here, a Monte Carlo simulation analysis of the 20% discount is a fairly straightforward analysis and, consequently, it is difficult for us to believe three sets of casino statisticians miscalculated.
It is difficult without being able to reproduce the original paper to give this quote the correct context. I strongly disagree with the sentiment as expressed by the subset of language I've extracted above.
Without meaning to insult my industry, casinos do not employ statisticians skilled in Monte Carlo simulations. Indeed, in all my years working with the industry, I don’t know a single instance of a casino running a Monte Carlo simulation. The casino industry truly needs trained professionals with advanced degrees in statistics, skilled in the mathematics of a wide range of casino games, who have deep computer programming experience. As many in the casino industry have found out the hard way, even professionals with apparent expertise can have a hard time getting it right.
The first step in any research project is a literature search. It appears that the authors did not do a simple Google search. If they had searched “Donald Johnson blackjack” then they would have found any number of articles and message board discussions on the topic. This information would have provided ample evidence that both their thesis and conclusions were misguided. With such a search, they would have also found my work on the topic, which would have been high up on the first page of their Google search.
To continue their research, the authors could have called the casinos where DJ played to double-check his win amounts. Outreach to the magazines to research their fact-checking was a reasonable step. Directly contacting Bowden and Wittkowski for their comments and review was appropriate. The authors could have tried to contact DJ himself. The authors appear to have made no effort to get information on the events that took place beyond the two articles they read.
In the final paragraph, the authors disclaim the entirety of their research:
It is also possible that some key facts were not reported and thus the picture is incomplete or a set of assumptions is incorrect.
Publishing academic work is not like a Sunday opinion article. A standard of academic rigor is expected from University professors. The authors should either do the necessary research to have confidence in their conclusions or else they should not publish.
The authors conclude their article with this parting shot:
In any case, the firm conclusion of this study is that there is a role for probabilistic fact-checking at high-end periodicals.
I concur.


