
HIT FREQUENCY

The concept of "hit frequency" is best applied to games that pay “X-for-1” like keno, lotteries, slots and video poker. It is a little fuzzier when applied to table games, especially those with a strategy or multiple wagering opportunities.
If the player is playing keno, the lottery, slots or video poker then the player makes a bet (say $1). That $1 is forfeit. It's gone. Now the only question is if he will get something back after the round has resolved. Sometimes yes, sometimes no. In the real world, nothing is exact. But to the mathematician analyzing these games, they can determine very exact numbers. We’ll use Keno as an example.
Suppose you are playing Keno and you mark 10 spots on a card with 80 spots. Suppose 20 balls are dropped in the Keno game. This is all very standard, exactly how Keno usually works in many casinos.
Now suppose the pay table for Keno awards some money back if you hit 3 or more of the 10 spots you marked. You always lose your original bet. It's gone. The question is if you get to collect anything at the end of the ball drop. It's time for decimals and percents. Don't ask me how I figured it out, but for this exact situation the hit frequency (probability of 3 or more hits) is 47.94%, or 0.4794. If we modify the Keno pay table so that it pays back only when you hit 4 or more of the 10 spots you marked, then the hit frequency is 21.20%, or 0.2120. If we have a payout any time 2 or more of the 10 spots are hit, then the hit frequency is 77.46%, or 0.7746..


For the Pair Plus wager, the number 25.61% is an exact number. The hit frequency is a theoretical number; it is computed by a mathematician. In practice, it gives a good sense for how the game will perform on the floor, but the game’s actual performance has nothing to do with determining the hit frequency.
The hit frequency gives a sense of how often a player is going to get something back on his wager. Obviously a player wants to win as often as possible, so from the player’s perspective a high hit frequency is a good thing. Naturally, the player also wants high payouts. These two desires act against each other: giving the player everything he wants is impossible.
A game that has a low hit frequency with high payouts may frustrate the player because he seems to lose and lose while waiting for a combination to occur that seems ever more unlikely. A game that has a high hit frequency with low payouts may frustrate the player because he feels like he is going nowhere fast; it becomes obvious how the house is making its money. The answer is always somewhere in between.
We are going to create two lottery games to illustrate these psychological points. A low hit frequency, high payout lottery and a high hit frequency, low payout lottery. We’ve designed these as extreme examples just to drive home the point about how this feels from the player’s perspective.
Suppose we’ve been given the task of creating a lottery with one million tickets; the cost of each ticket is one dollar. We know that if we sell every ticket, then we will take in $1,000,000 gross income. We are directed to return $900,000 in cash prizes, leaving a net profit of $100,000. We consider two prize schemes.

EXAMPLE: LOTTERY 1 (LOW HIT FREQUENCY, HIGH PAYOUT):
One million tickets are produced. Each costs $1 to play. Out of these 1 million tickets, suppose exactly 9 of them pay 100,000-for-1 and the others lose. That is, 9 of them say "You win $100,000!" and the other 999,991 of them say "Please play again!” The player will consider the $1 purchase of the ticket measured against the possibility of winning $100,000.
In this case the hit frequency is 9/1,000,000 = 0.0009%.

EXAMPLE: LOTTERY 2 (HIGH HIT FREQUENCY, LOW PAYOUT):
One million tickets are produced. Each costs $1 to play. Out of these 1 million tickets, suppose exactly 900,000 pay 1-for-1 and the others lose. That is, 900,000 of them say "You win $1!" and the other 100,000 say "Please play again!" The player will consider the $1 purchase of a ticket measured against the possibility of winning $1.
In this case the hit frequency is 900,000/1,000,000 = 90.00%.
It is easy to see that each lottery makes the same amount of profit if every ticket is sold. Lottery players like the opportunity to win big, so lottery 1 is more likely to succeed in the marketplace. But if lottery 1 was a casino game, player after player would lose his entire buy-in a matter of minutes (even playing just $1 per round). A few players would win big eventually, but that would be extremely rare. The game would die soon after it was put on the floor. If a casino game was designed in lottery 2 style, players might play for the entertainment and free drinks, but that game too would not last long. Players of lottery 2 have no chance to ever get ahead of the game.
Hit frequencies, as described above, are precisely defined for keno, lotteries, slots and video poker. This term also has this meaning for certain wagers that pay for a specific hand or event at a table game. As we saw above, it makes sense to discuss the hit frequency for the Pair Plus wager in Three Card Poker. What does “hit frequency” mean for a more complicated wager involving strategy at a table game?
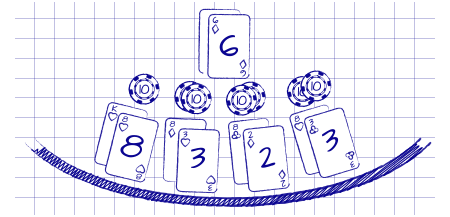 Suppose you are playing blackjack. You place a $10 bet and are dealt 8-8 against the dealer's 6. You split and re-split to four hands. You double on three of the four splits. You put out a total of $70 on the hand. A lot of other stuff happens and you look down at the end of what you’ve been paid. Either there is more than $70 in front of you, less than $70, or you managed to get a big push and have $70 returned to you. What does "hit frequency" mean in a situation like this? Honestly, I have no idea. No matter how ill-defined, hit frequency has become part of the vernacular of table games. Some features of games have hit frequencies that can be computed. In many cases, hit frequency just doesn't make sense according to the formal definition.
Suppose you are playing blackjack. You place a $10 bet and are dealt 8-8 against the dealer's 6. You split and re-split to four hands. You double on three of the four splits. You put out a total of $70 on the hand. A lot of other stuff happens and you look down at the end of what you’ve been paid. Either there is more than $70 in front of you, less than $70, or you managed to get a big push and have $70 returned to you. What does "hit frequency" mean in a situation like this? Honestly, I have no idea. No matter how ill-defined, hit frequency has become part of the vernacular of table games. Some features of games have hit frequencies that can be computed. In many cases, hit frequency just doesn't make sense according to the formal definition.






